Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

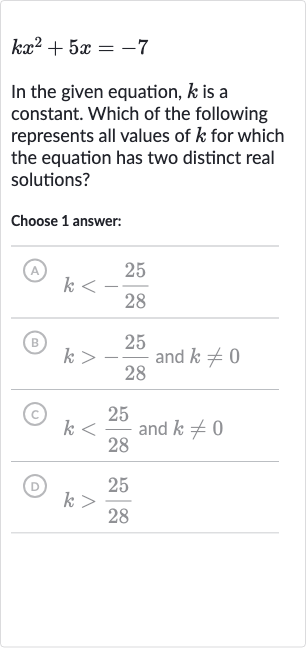
kx^(2)+5x=-7 In the given equation, k is a constant. Which of the following represents all values of k for which the equation has two distinct real solutions? Choose 1 answer: (A) k < -(25)/(28) (B) k > -(25)/(28) and k!=0 (c) k < (25)/(28) and k!=0 (D) k > (25)/(28)

kx2+5x=−7 k x^{2}+5 x=-7 \newlineIn the given equation, k k is a constant. Which of the following represents all values of k k for which the equation has two distinct real solutions?\newlineChoose 11 answer:\newline(A) k<-\frac{25}{28} \newline(B) k>-\frac{25}{28} and k≠0 k \neq 0 \newline(C) k<\frac{25}{28} and k≠0 k \neq 0 \newline(D) k>\frac{25}{28}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of absolute value functions: translations and reflectionsright chevron icon

Full solution

Q. kx2+5x=−7 k x^{2}+5 x=-7 \newlineIn the given equation, k k is a constant. Which of the following represents all values of k k for which the equation has two distinct real solutions?\newlineChoose 11 answer:\newline(A) k<−2528 k<-\frac{25}{28} \newline(B) k>−2528 k>-\frac{25}{28} and k≠0 k \neq 0 \newline(C) k<2528 k<\frac{25}{28} and k≠0 k \neq 0 \newline(D) k>2528 k>\frac{25}{28}
  1. Determine Conditions: We need to determine the conditions under which the quadratic equation kx2+5x+7=0kx^2 + 5x + 7 = 0 has two distinct real solutions. This depends on the discriminant, which is given by the formula D=b2−4acD = b^2 - 4ac, where aa, bb, and cc are the coefficients of x2x^2, xx, and the constant term, respectively.
  2. Calculate Discriminant: For the equation kx2+5x+7=0kx^2 + 5x + 7 = 0, a=ka = k, b=5b = 5, and c=7c = 7. Let's calculate the discriminant DD.\newlineD=b2−4ac=(5)2−4(k)(7)=25−28kD = b^2 - 4ac = (5)^2 - 4(k)(7) = 25 - 28k.
  3. Discriminant Greater Than Zero: For the equation to have two distinct real solutions, the discriminant must be greater than zero. Therefore, we need D > 0.25 - 28k > 0.
  4. Solve Inequality for k: Solving the inequality for k, we get:\newline-28k > -25\newlinek < \frac{25}{28}.
  5. Consider Exclusion of k=0k=0: However, we must also remember that kk cannot be zero because if k=0k = 0, the equation becomes linear, not quadratic. Therefore, kk must also be different from zero.
  6. Combine Conditions: Combining the conditions, we find that kk must be less than 2528\frac{25}{28} and not equal to zero for the equation to have two distinct real solutions.

More problems from Transformations of absolute value functions: translations and reflections

Question
Find g(x) g(x) , where g(x) g(x) is the translation 2 2 units left of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the reflection across the y y -axis of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 77 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=7∣x∣ y=7|x| \newline(B) y=−7∣x∣ y=-7|x| \newlineC) y=17∣x∣ y=\frac{1}{7}|x| \newline(D) y=−17∣x∣ y=-\frac{1}{7}|x|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 66 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x−6∣ y=|x-6| \newline(B) y=6∣x∣ y=6|x| \newline(C) y=16∣x∣ y=\frac{1}{6}|x| \newline(D) y=∣x−16∣ y=\left|x-\frac{1}{6}\right|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 13 \frac{1}{3} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−3 y=|x|-3 \newline(B) y=−3∣x∣ y=-3|x| \newline(C) y=13∣x∣ y=\frac{1}{3}|x| \newline(D) y=∣x∣−13 y=|x|-\frac{1}{3}
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted to the left by 66 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x+6∣−6 y=|x+6|-6 \newline(B) y=∣x−6∣−6 y=|x-6|-6 \newline(C) y=∣x∣−6 y=|x|-6 \newline(D) y=∣x+6∣ y=|x+6|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 14 \frac{1}{4} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=−4∣x∣ y=-4|x| \newline(B) y=∣x∣−4 y=|x|-4 \newline(C) y=−14∣x∣ y=-\frac{1}{4}|x| \newline(D) y=∣x−4∣ y=|x-4|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted down by 99 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−9 y=|x|-9 \newline(B) y=∣x+9∣ y=|x+9| \newline(C) y=∣x∣+9 y=|x|+9 \newline(D) y=∣x−9∣ y=|x-9|
Get tutor helpright-arrow

Posted 10 months ago

Question
y=13x+5y=2x \begin{array}{l} y=\frac{1}{3} x+5 \\ y=2 x \end{array} \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of y+x y+x ?
Get tutor helpright-arrow

Posted 3 months ago

Question
13x+3y=4 \frac{1}{3} x+3 y=4 \newline2x−4=2y 2 x-4=2 y \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of x−y x-y ?
Get tutor helpright-arrow

Posted 2 months ago

View all (49)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant