Full solution
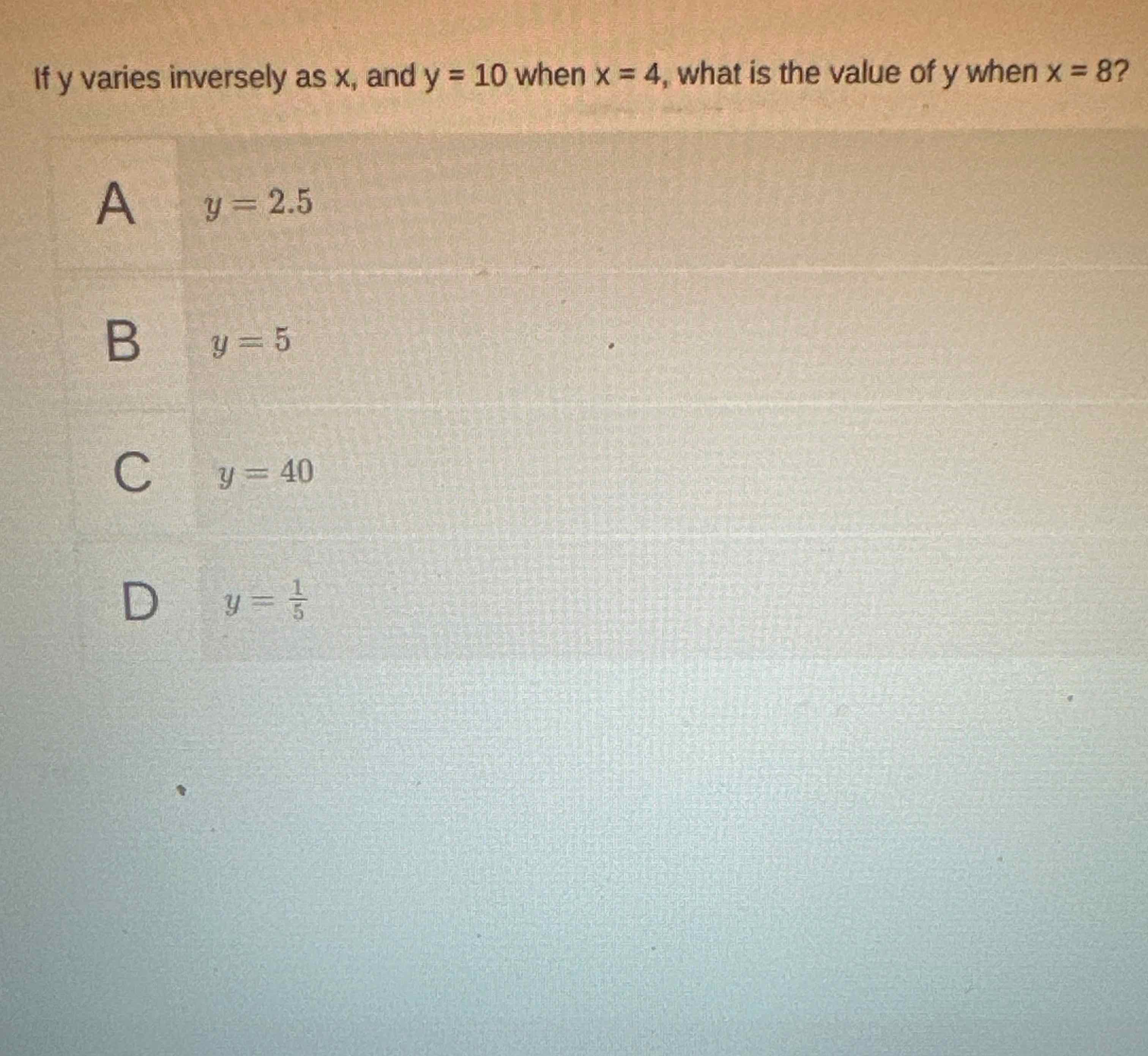
Q. If varies inversely as , and when , what is the value of when ?A) B) C) D)
- Given Inverse Variation: Given that varies inversely as . This means where is a constant.
- Find Constant : We know when . Substitute these values to find . .
- Write Variation Equation: Solve for : Multiply both sides by to isolate . . .
- Find for : Now, use the found value of to write the inverse variation equation. .
- Find for : Now, use the found value of to write the inverse variation equation. . To find when , substitute for in the equation. . .
More problems from Write and solve inverse variation equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor help