AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
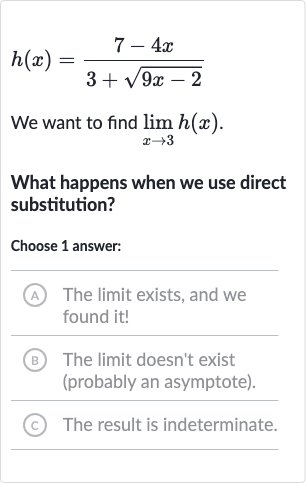
We want to find .What happens when we use direct substitution?Choose answer:(A) The limit exists, and we found it!(B) The limit doesn't exist (probably an asymptote).(C) The result is indeterminate.
Full solution
Q. We want to find .What happens when we use direct substitution?Choose answer:(A) The limit exists, and we found it!(B) The limit doesn't exist (probably an asymptote).(C) The result is indeterminate.
- Plug : Let's try direct substitution by plugging into .
- Simplify numerator and denominator: Simplify the numerator and the denominator.
- Continue simplifying: Continue simplifying.
- Simplify square root: Simplify the square root.
- Add numbers in denominator: Add the numbers in the denominator.
- Limit exists, answer is : So, the limit exists and we found it by direct substitution.The answer is The limit exists, and we found it!
More problems from Write and solve inverse variation equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor help