Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

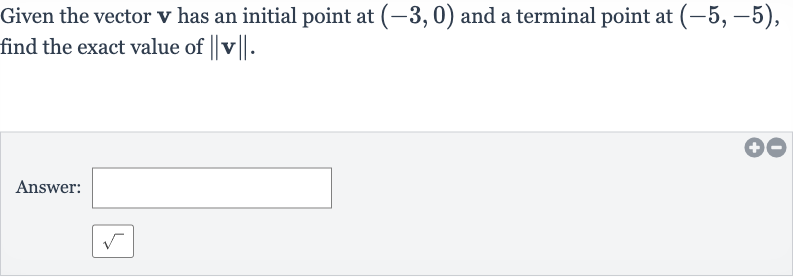
Given the vector v has an initial point at (-3,0) and a terminal point at (-5,-5), find the exact value of ||v||. Answer:

Given the vector v \mathbf{v} has an initial point at (−3,0) (-3,0) and a terminal point at (−5,−5) (-5,-5) , find the exact value of ∥v∥ \|\mathbf{v}\| .\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of absolute value functions: translations and reflectionsright chevron icon

Full solution

Q. Given the vector v \mathbf{v} has an initial point at (−3,0) (-3,0) and a terminal point at (−5,−5) (-5,-5) , find the exact value of ∥v∥ \|\mathbf{v}\| .\newlineAnswer:
  1. Use Distance Formula: To find the magnitude of vector vv, we need to use the distance formula, which is derived from the Pythagorean theorem. The distance formula for a vector with initial point (x1,y1)(x_1, y_1) and terminal point (x2,y2)(x_2, y_2) is:\newline∣∣v∣∣=((x2−x1)2+(y2−y1)2)||v|| = \sqrt{((x_2 - x_1)^2 + (y_2 - y_1)^2)}
  2. Substitute Given Points: Substitute the given points into the distance formula:\newlineInitial point (x1,y1)=(−3,0)(x_1, y_1) = (-3, 0)\newlineTerminal point (x2,y2)=(−5,−5)(x_2, y_2) = (-5, -5)\newline∣∣v∣∣=((−5−(−3))2+(−5−0)2)||v|| = \sqrt{((-5 - (-3))^2 + (-5 - 0)^2)}
  3. Simplify Expression: Simplify the expression inside the square root:\newline||v|| = \sqrt{((\(-5\) + \(3\))^\(2\) + (\(-5\))^\(2\))}\(\newline||v|| = \sqrt{(22^22 + (−5-5)^22)}\newline||v|| = \sqrt{(44 + 2525)}
  4. Find Magnitude: Add the squares to find the magnitude:\newline∣∣v∣∣=29||v|| = \sqrt{29}\newlineSince 2929 is a prime number, it cannot be simplified further, so the exact value of the magnitude of vector vv is 29\sqrt{29}.

More problems from Transformations of absolute value functions: translations and reflections

Question
Find g(x) g(x) , where g(x) g(x) is the translation 2 2 units left of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the reflection across the y y -axis of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 77 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=7∣x∣ y=7|x| \newline(B) y=−7∣x∣ y=-7|x| \newlineC) y=17∣x∣ y=\frac{1}{7}|x| \newline(D) y=−17∣x∣ y=-\frac{1}{7}|x|
Get tutor helpright-arrow

Posted 2 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 66 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x−6∣ y=|x-6| \newline(B) y=6∣x∣ y=6|x| \newline(C) y=16∣x∣ y=\frac{1}{6}|x| \newline(D) y=∣x−16∣ y=\left|x-\frac{1}{6}\right|
Get tutor helpright-arrow

Posted 1 month ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 13 \frac{1}{3} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−3 y=|x|-3 \newline(B) y=−3∣x∣ y=-3|x| \newline(C) y=13∣x∣ y=\frac{1}{3}|x| \newline(D) y=∣x∣−13 y=|x|-\frac{1}{3}
Get tutor helpright-arrow

Posted 2 months ago

Question
The graph of y=∣x∣ y=|x| is shifted to the left by 66 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x+6∣−6 y=|x+6|-6 \newline(B) y=∣x−6∣−6 y=|x-6|-6 \newline(C) y=∣x∣−6 y=|x|-6 \newline(D) y=∣x+6∣ y=|x+6|
Get tutor helpright-arrow

Posted 1 month ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 14 \frac{1}{4} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=−4∣x∣ y=-4|x| \newline(B) y=∣x∣−4 y=|x|-4 \newline(C) y=−14∣x∣ y=-\frac{1}{4}|x| \newline(D) y=∣x−4∣ y=|x-4|
Get tutor helpright-arrow

Posted 2 months ago

Question
The graph of y=∣x∣ y=|x| is shifted down by 99 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−9 y=|x|-9 \newline(B) y=∣x+9∣ y=|x+9| \newline(C) y=∣x∣+9 y=|x|+9 \newline(D) y=∣x−9∣ y=|x-9|
Get tutor helpright-arrow

Posted 4 months ago

Question
y=13x+5y=2x \begin{array}{l} y=\frac{1}{3} x+5 \\ y=2 x \end{array} \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of y+x y+x ?
Get tutor helpright-arrow

Posted 1 month ago

Question
13x+3y=4 \frac{1}{3} x+3 y=4 \newline2x−4=2y 2 x-4=2 y \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of x−y x-y ?
Get tutor helpright-arrow

Posted 1 month ago

View all (56)