Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

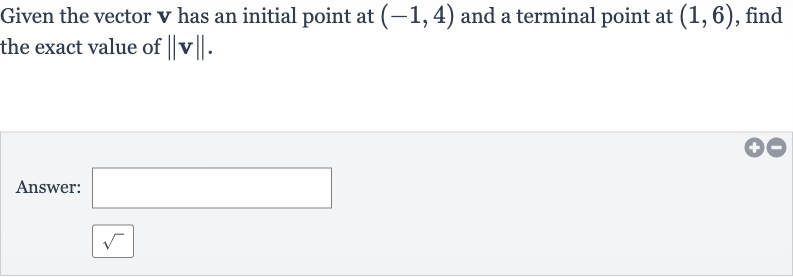
Given the vector v has an initial point at (-1,4) and a terminal point at (1,6), find the exact value of ||v||. Answer:

Given the vector v \mathbf{v} has an initial point at (−1,4) (-1,4) and a terminal point at (1,6) (1,6) , find the exact value of ∥v∥ \|\mathbf{v}\| .\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of absolute value functions: translations and reflectionsright chevron icon

Full solution

Q. Given the vector v \mathbf{v} has an initial point at (−1,4) (-1,4) and a terminal point at (1,6) (1,6) , find the exact value of ∥v∥ \|\mathbf{v}\| .\newlineAnswer:
  1. Calculate Differences: To find the magnitude of the vector vv, we need to calculate the difference in the xx-coordinates and the difference in the yy-coordinates between the terminal point and the initial point. The magnitude ∣∣v∣∣||v|| is the square root of the sum of the squares of these differences.\newlineLet's denote the initial point as (x1,y1)=(−1,4)(x_1, y_1) = (-1, 4) and the terminal point as (x2,y2)=(1,6)(x_2, y_2) = (1, 6). The differences are Δx=x2−x1\Delta x = x_2 - x_1 and Δy=y2−y1\Delta y = y_2 - y_1.
  2. Calculate Magnitude: Calculate Δx\Delta x and Δy\Delta y: \newlineΔx=1−(−1)=1+1=2\Delta x = 1 - (-1) = 1 + 1 = 2\newlineΔy=6−4=2\Delta y = 6 - 4 = 2\newlineNow we have the differences in the xx and yy coordinates.
  3. Use Pythagorean Theorem: Use the Pythagorean theorem to find the magnitude of the vector vv:∥v∥=(Δx2+Δy2)\|v\| = \sqrt{(\Delta x^2 + \Delta y^2)}Substitute Δx\Delta x and Δy\Delta y into the equation:∥v∥=(22+22)\|v\| = \sqrt{(2^2 + 2^2)}
  4. Calculate Sum: Calculate the squares of Δx\Delta x and Δy\Delta y and their sum:\newline∣∣v∣∣=4+4||v|| = \sqrt{4 + 4}\newline∣∣v∣∣=8||v|| = \sqrt{8}
  5. Simplify Square Root: Simplify the square root to find the exact value of ∣∣v∣∣||v||:∣∣v∣∣=(4×2)||v|| = \sqrt{(4 \times 2)}∣∣v∣∣=22||v|| = 2\sqrt{2}This is the exact value of the magnitude of vector vv.

More problems from Transformations of absolute value functions: translations and reflections

Question
Find g(x) g(x) , where g(x) g(x) is the translation 2 2 units left of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the reflection across the y y -axis of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 77 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=7∣x∣ y=7|x| \newline(B) y=−7∣x∣ y=-7|x| \newlineC) y=17∣x∣ y=\frac{1}{7}|x| \newline(D) y=−17∣x∣ y=-\frac{1}{7}|x|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 66 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x−6∣ y=|x-6| \newline(B) y=6∣x∣ y=6|x| \newline(C) y=16∣x∣ y=\frac{1}{6}|x| \newline(D) y=∣x−16∣ y=\left|x-\frac{1}{6}\right|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 13 \frac{1}{3} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−3 y=|x|-3 \newline(B) y=−3∣x∣ y=-3|x| \newline(C) y=13∣x∣ y=\frac{1}{3}|x| \newline(D) y=∣x∣−13 y=|x|-\frac{1}{3}
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted to the left by 66 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x+6∣−6 y=|x+6|-6 \newline(B) y=∣x−6∣−6 y=|x-6|-6 \newline(C) y=∣x∣−6 y=|x|-6 \newline(D) y=∣x+6∣ y=|x+6|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 14 \frac{1}{4} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=−4∣x∣ y=-4|x| \newline(B) y=∣x∣−4 y=|x|-4 \newline(C) y=−14∣x∣ y=-\frac{1}{4}|x| \newline(D) y=∣x−4∣ y=|x-4|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted down by 99 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−9 y=|x|-9 \newline(B) y=∣x+9∣ y=|x+9| \newline(C) y=∣x∣+9 y=|x|+9 \newline(D) y=∣x−9∣ y=|x-9|
Get tutor helpright-arrow

Posted 10 months ago

Question
y=13x+5y=2x \begin{array}{l} y=\frac{1}{3} x+5 \\ y=2 x \end{array} \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of y+x y+x ?
Get tutor helpright-arrow

Posted 3 months ago

Question
13x+3y=4 \frac{1}{3} x+3 y=4 \newline2x−4=2y 2 x-4=2 y \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of x−y x-y ?
Get tutor helpright-arrow

Posted 2 months ago

View all (49)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant