Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the substitutions
ln 2=a,ln 3=b, and
ln 5=c, find the value of
ln((25)/(27)) in terms of
a,b, and
c.
Answer:

Given the substitutions $\ln 2=a, \ln 3=b$ , and $\ln 5=c$ , find the value of $\ln \left(\frac{25}{27}\right)$ in terms of $a, b$ , and $c$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Write and solve inverse variation equations

Full solution

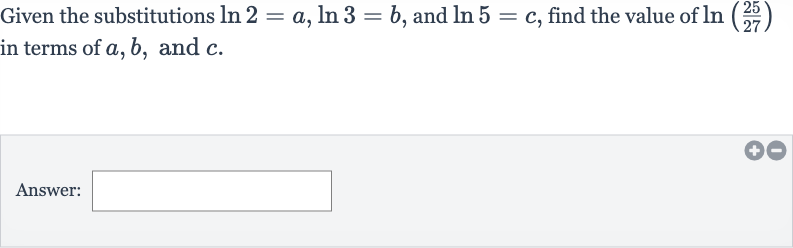
Q. Given the substitutions

\ln 2=a, \ln 3=b

, and

\ln 5=c

, find the value of

\ln \left(\frac{25}{27}\right)

in terms of

a, b

, and

c

.

\newline

Answer:

Rewrite using substitutions: Given that $\ln 2 = a$ , $\ln 3 = b$ , and $\ln 5 = c$ , we need to express $\ln\left(\frac{25}{27}\right)$ using these substitutions. $\newline$ First, we can rewrite $25$ as $5^2$ and $27$ as $3^3$ . $\newline$ So, $\ln\left(\frac{25}{27}\right)$ becomes $\ln\left(\frac{5^2}{3^3}\right)$ .
Separate terms in logarithm: Using the properties of logarithms, we can separate the terms in the logarithm. $\ln\left(\frac{5^2}{3^3}\right) = \ln(5^2) - \ln(3^3)$ .
Apply power rule of logarithms: Now, apply the power rule of logarithms, which states that $\ln(x^y) = y \cdot \ln(x)$ . This gives us $2 \cdot \ln(5) - 3 \cdot \ln(3)$ .
Substitute given values: Substitute the given values for $\ln(5)$ and $\ln(3)$ . This results in $2 \times c - 3 \times b$ .
Final answer: The expression $2 \times c - 3 \times b$ is the final answer in terms of $a$ , $b$ , and $c$ .

More problems from Write and solve inverse variation equations

Question

In a direct variation,

y = 6

x = 2

. Write a direct variation equation that shows the relationship between

x

y

\newline

Write your answer as an equation with

y

first, followed by an equals sign.

Posted 3 months ago

Question

y

varies directly with

x

y = 12

x = 6

y

x = 4

\newline

Write and solve a direct variation equation to find the answer.

\newline

y =

Posted 2 months ago

Question

Which equation shows inverse variation?

\newline

\newline

(\frac{x}{36}) = y

\newline

yx = -74

Posted 3 months ago

Question

y

varies inversely with

x

y = 1

x = 4

y

x = 2

\newline

Write and solve an inverse variation equation to find the answer.

\newline

y =

Posted 2 months ago

Question

What is the value of

\frac{x^{2}}{y^{4}}

x=8

y=2

Posted 24 days ago

Question

(x+4)(2 x-a)=0

\newline

In the given equation,

a

is a constant. If the equation has the solutions

x=4

x=-4

, what is the value of

a

Posted 2 months ago

Question

(2 x+5)(-m x+9)=0

\newline

In the given equation,

m

is a constant. If the equation has the solutions

x=-\frac{5}{2}

x=\frac{3}{2}

, what is the value of

m

Posted 2 months ago

Question

(4 x+3)-(5 x-7)=a x+b

\newline

In the given equation,

b

is a constant. What is the value of

b

Posted 2 months ago

Question

y=\frac{29}{8} x-\frac{2}{3}

\newline

The given equation is graphed in the

x y

-plane. What is the slope of the line?

Posted 2 months ago

Question

a t^{2}+\frac{7}{2} t-4=0

\newline

The given equation has solutions at

t=-8

t=1

. What is the value of the constant

a

Posted 2 months ago