Full solution
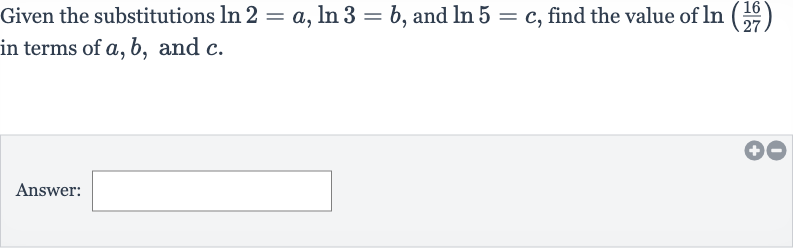
Q. Given the substitutions , and , find the value of in terms of , and .Answer:
- Rewrite in Prime Factors: Given that , , and , we need to express using these substitutions.First, we can rewrite and in terms of their prime factors: and .So, becomes .Using the properties of logarithms, we can express this as .
- Apply Power Rule: Now, we apply the power rule of logarithms, which states that , to both terms.This gives us .
- Substitute Given Values: Substitute the given values for and , which are and respectively.This results in .
- Final Expression: We have now expressed in terms of and . Since is not needed to express , we do not use it in our final expression.
More problems from Write and solve inverse variation equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor help