AI tutor
Full solution
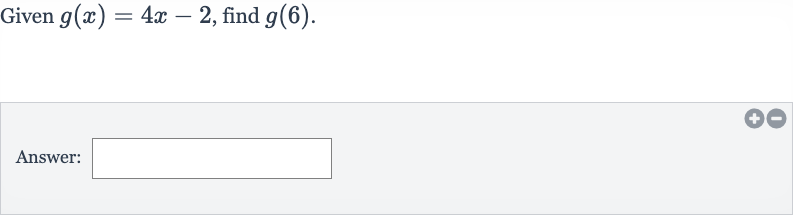
Q. Given , find .Answer:
- Substitute with : To find the value of , we need to substitute with in the function .Calculation:
- Perform multiplication and subtraction: Now, we perform the multiplication and subtraction to get the value of .Calculation:
- Final subtraction for answer: Finally, we subtract from to get the final answer.Calculation: