Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the derivative of the following function.

y=log_(2)(2x^(2)+2x)
Answer:
y^(')=

Find the derivative of the following function. $\newline$ $y=\log _{2}\left(2 x^{2}+2 x\right)$ $\newline$ Answer: $y^{\prime}=$

View step-by-step help

View step-by-step help

Find derivatives using logarithmic differentiation

Full solution

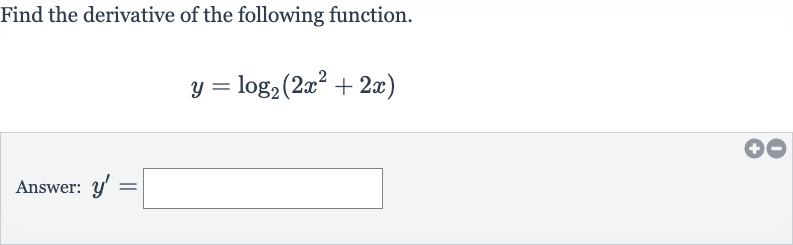
Q. Find the derivative of the following function.

\newline

y=\log _{2}\left(2 x^{2}+2 x\right)

\newline

Answer:

y^{\prime}=

Apply Chain Rule: First, we need to apply the chain rule for derivatives, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. The outer function here is $\log_2(u)$ , and the inner function is $u = 2x^2 + 2x$ .
Differentiate $\log_2(u)$ : To differentiate $\log_2(u)$ with respect to $u$ , we use the formula $\frac{d}{dx} [\log_2(u)] = \frac{1}{(u \ln(2))}$ . This is because the derivative of log base $a$ of $u$ is $\frac{1}{(u \ln(a))}$ , where $\ln$ denotes the natural logarithm.
Find Derivative of Inner Function: Now we need to find the derivative of the inner function $u = 2x^2 + 2x$ with respect to $x$ . Using the power rule, the derivative of $x^2$ is $2x$ , and the derivative of $x$ is $1$ . Therefore, the derivative of $u$ with respect to $x$ is $\frac{du}{dx} = 2(2x) + 2(1) = 4x + 2$ .
Combine Results: Combining the results from the previous steps, we get the derivative of $y$ with respect to $x$ as $y' = \frac{1}{(2x^2 + 2x \ln(2))} \cdot (4x + 2)$ .
Simplify Expression: We can simplify the expression by factoring out $2$ from the numerator and denominator. This gives us $y' = \frac{2(2x + 1)}{2(2x^2 + 2x) \ln(2)} = \frac{2x + 1}{(2x^2 + 2x) \ln(2)}$ .

More problems from Find derivatives using logarithmic differentiation

Question

\newline

\sqrt{\frac{9}{25}}

\newline

Posted 2 months ago

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 2 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 2 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 2 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 2 months ago

Question

\newline

500

=

Posted 3 months ago

Question

\newline

2,000

=

Posted 3 months ago

Question

\newline

750

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago