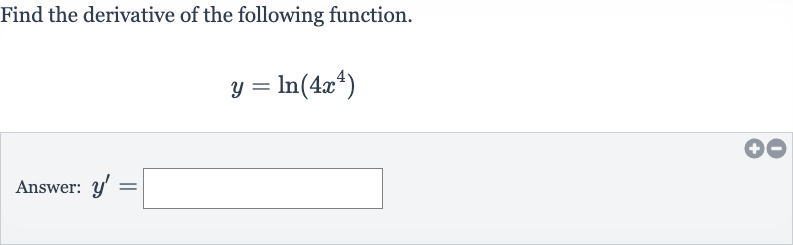
Find the derivative of the following function. y=ln(4x^(4)) Answer: y^(')=

Question

Find the derivative of the following function.  y=ln(4x^(4)) Answer:  y^(')=

Bytelearn · Accepted Answer

Apply Chain Rule: Apply the chain rule for differentiation. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. For y = ln(4x^(4)), the outer function is ln(u) and the inner function is u = 4x^(4). First, we find the derivative of the outer function with respect to its argument u, which is 1/u. Then, we will find the derivative of the inner function with respect to x, which is the derivative of 4x^(4).Differentiate Inner Function: Differentiate the inner function 4x^(4) with respect to x. Using the power rule, which states that the derivative of x^n with respect to x is n*x^(n-1), we differentiate 4x^(4). The derivative of 4x^(4) with respect to x is 4 * 4x^(3) = 16x^(3).Combine Derivatives: Combine the derivatives of the outer and inner functions using the chain rule. The derivative of y with respect to x is the derivative of the outer function times the derivative of the inner function. So, y' = (1/u) * (16x^(3)), where u = 4x^(4).Substitute u: Substitute u back into the derivative. Since u = 4x^(4), we substitute it back into the expression for y'. y' = (1/(4x^(4))) * (16x^(3)).Simplify Expression: Simplify the expression. We can simplify the expression by canceling out common factors. y' = (16x^(3)) / (4x^(4)) = 4x^(3) / x^(4).Cancel x Terms: Simplify the expression further by canceling x terms. When dividing powers with the same base, we subtract the exponents. y' = 4 / x^(4-3) = 4 / x.

Find the derivative of the following function. $\newline$ $y=\ln \left(4 x^{4}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Find derivatives using logarithmic differentiation

Related topics

Find the derivative of the following function.\newliney=ln⁡(4x4) y=\ln \left(4 x^{4}\right) y=ln(4x4)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\ln \left(4 x^{4}\right)$ $\newline$ Answer: $y^{\prime}=$