Full solution
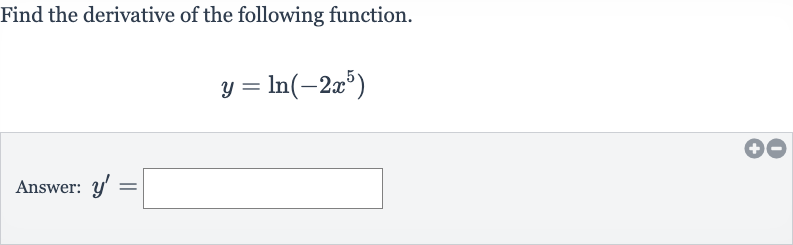
Q. Find the derivative of the following function.Answer:
- Identify Function: Identify the function to differentiate.We are given the function . We need to find its derivative with respect to .
- Apply Chain Rule: Apply the chain rule for differentiation.The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. In this case, the outer function is and the inner function is .
- Differentiate Outer Function: Differentiate the outer function.The derivative of with respect to is . So, the derivative of with respect to is .
- Differentiate Inner Function: Differentiate the inner function.The derivative of with respect to is , using the power rule which states that the derivative of is .
- Multiply Derivatives: Multiply the derivatives from Step and Step .We multiply the derivative of the outer function by the derivative of the inner function to get the overall derivative: .
- Simplify Expression: Simplify the expression.When we multiply , we get which simplifies to .