Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the derivative of the following function.

y=e^(5x^(5))
Answer:
y^(')=

Find the derivative of the following function. $\newline$ $y=e^{5 x^{5}}$ $\newline$ Answer: $y^{\prime}=$

View step-by-step help

View step-by-step help

Find derivatives using logarithmic differentiation

Full solution

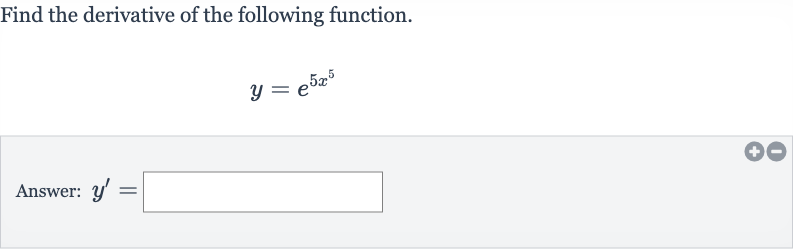
Q. Find the derivative of the following function.

\newline

y=e^{5 x^{5}}

\newline

Answer:

y^{\prime}=

Identify Function & Rule: Identify the function and the rule to use for differentiation. $\newline$ We have the function $y=e^{5x^{5}}$ . To find the derivative, we will use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
Apply Chain Rule: Apply the chain rule to differentiate the function. The outer function is $e^u$ where $u=5x^{5}$ . The derivative of $e^u$ with respect to $u$ is $e^u$ . The inner function is $u=5x^{5}$ . The derivative of $u$ with respect to $x$ is $5\cdot(5x^{5-1})=25x^{4}$ . Now, we multiply the derivative of the outer function by the derivative of the inner function. $y' = e^{5x^{5}} \cdot 25x^{4}$
Simplify Derivative: Simplify the expression for the derivative. $\newline$ $y' = 25x^{4} \cdot e^{5x^{5}}$ $\newline$ This is the simplified form of the derivative.

More problems from Find derivatives using logarithmic differentiation

Question

\newline

\sqrt{\frac{9}{25}}

\newline

Posted 2 months ago

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 2 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 2 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 2 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 2 months ago

Question

\newline

500

=

Posted 3 months ago

Question

\newline

2,000

=

Posted 3 months ago

Question

\newline

750

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago