Full solution
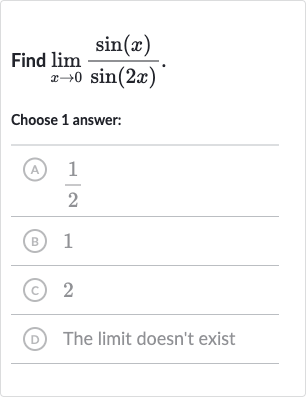
Q. Find .Choose answer:(A) (B) (C) (D) The limit doesn't exist
- Apply Limit Directly: We need to find the limit of the function as approaches . We can start by applying the limit to the function directly.
- Identify Indeterminate Form: We notice that if we directly substitute into the function, we get , which is an indeterminate form . This means we cannot directly evaluate the limit by substitution.
- Use Trigonometric Identity: To resolve the indeterminate form, we can use the trigonometric identity to rewrite the denominator.
- Simplify Expression: We can now simplify the expression by canceling out the common term in the numerator and denominator, as long as is not equal to (since , we cannot divide by zero).
- Substitute : Now that we have simplified the expression, we can directly substitute into the remaining function, as is continuous at .