Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

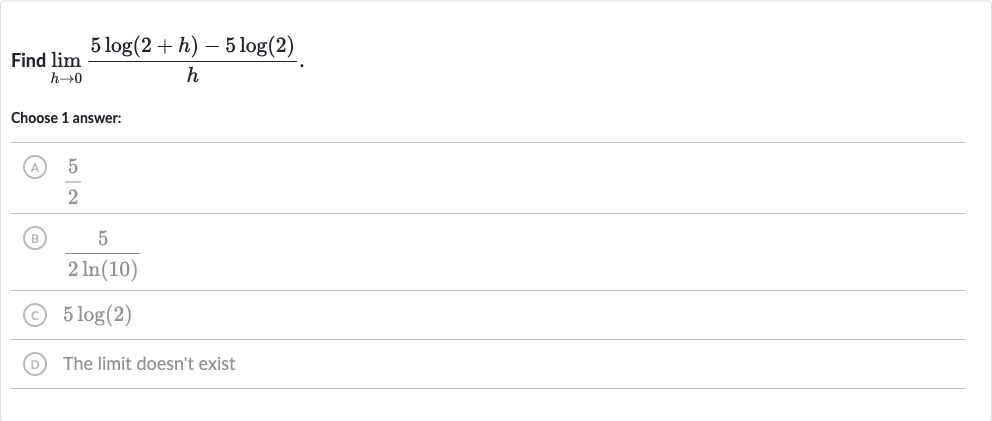
Find
lim_(h rarr0)(5log(2+h)-5log(2))/(h).
Choose 1 answer:
(A)
(5)/(2)
(B)
(5)/(2ln(10))
(C)
5log(2)
(D) The limit doesn't exist

Find $\lim _{h \rightarrow 0} \frac{5 \log (2+h)-5 \log (2)}{h}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{5}{2}$ $\newline$ (B) $\frac{5}{2 \ln (10)}$ $\newline$ (C) $5 \log (2)$ $\newline$ (D) The limit doesn't exist

View step-by-step help

View step-by-step help

Find derivatives of logarithmic functions

Full solution

Q. Find

\lim _{h \rightarrow 0} \frac{5 \log (2+h)-5 \log (2)}{h}

.

\newline

Choose

1

answer:

\newline

(A)

\frac{5}{2}

\newline

(B)

\frac{5}{2 \ln (10)}

\newline

(C)

5 \log (2)

\newline

(D) The limit doesn't exist

Combine logarithmic terms: Use the properties of logarithms to combine the terms in the numerator. $\lim_{h \rightarrow 0}\frac{5\log(2+h)-5\log(2)}{h} = \lim_{h \rightarrow 0}\frac{5\log\left(\frac{2+h}{2}\right)}{h}$
Apply constant multiple rule: Apply the constant multiple rule in limits to take the constant $5$ out of the limit. $\lim_{h \to 0}\left(\frac{5\log\left(\frac{2+h}{2}\right)}{h}\right) = 5 \times \lim_{h \to 0}\left(\frac{\log\left(\frac{2+h}{2}\right)}{h}\right)$
Use derivative definition: Use the definition of the derivative for the function $f(x) = \log(x)$ at $x = 2$ . $\lim_{h \to 0}\frac{\log((2+h)/2)}{h} = f'(2)$ where $f(x) = \log(x)$
Calculate derivative: The derivative of $\log(x)$ is $\frac{1}{x\ln(10)}$ . So, $f'(2) = \frac{1}{2\ln(10)}$ .
Multiply by constant: Multiply the derivative by the constant $5$ that we factored out earlier. $\newline$ $5 \times f'(2) = 5 \times \left(\frac{1}{2\ln(10)}\right) = \frac{5}{2\ln(10)}$

More problems from Find derivatives of logarithmic functions

Question

\lim_{\theta \rightarrow \frac{\pi}{2}} \tan ^{2}(\theta)[1-\sin (\theta)]

\newline

1

\newline

0

\newline

\frac{1}{2}

\newline

-2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{\theta \rightarrow \frac{\pi}{2}} \frac{\sin ^{2}(2 \theta)}{1-\sin ^{2}(\theta)}

\newline

1

\newline

1

\newline

2

\newline

4

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow 3} \frac{x-3}{\sqrt{4 x+4}-4}

\newline

1

\newline

-4

\newline

1

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow-4} \frac{7 x+28}{x^{2}+x-12}

\newline

1

\newline

1

\newline

7

\newline

-1

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow-3} \frac{x+3}{4-\sqrt{2 x+22}}

\newline

1

\newline

-3

\newline

-4

\newline

-\frac{3}{4}

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow 1} \frac{\sqrt{5 x+4}-3}{x-1}

\newline

1

\newline

\frac{3}{5}

\newline

\frac{5}{6}

\newline

1

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow-2} \frac{x^{3}+3 x^{2}+2 x}{x+2}

\newline

1

\newline

6

\newline

0

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cot ^{2}(x)}{1-\sin (x)}

\newline

1

\newline

-1

\newline

-\frac{\pi}{2}

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin (2 x)}{\cos (x)}

\newline

1

\newline

\frac{1}{2}

\newline

1

\newline

2

\newline

(D) The limit doesn't exist

Posted 3 months ago

Question

\lim _{\theta \rightarrow \frac{\pi}{4}} \frac{\cos (2 \theta)}{\sqrt{2} \cos (\theta)-1}

\newline

1

\newline

2

\newline

\frac{1}{2}

\newline

\sqrt{2}

\newline

(D) The limit doesn't exist

Posted 3 months ago