AI tutor
Full solution
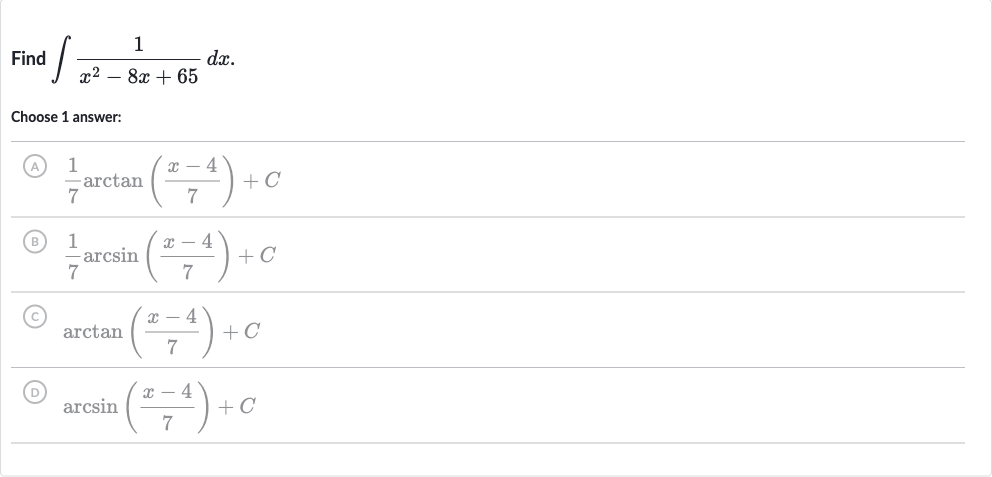
Q. Find .Choose answer:(A) (B) (C) (D)
- Complete the square: Complete the square for the denominator to make it look like , which is suitable for a trigonometric substitution.
- Recognize standard form: Recognize that the integral is now in the form of , which is a standard form for substitution.
- Use substitution : Use the substitution , then .
- Rewrite integral in terms: Rewrite the integral in terms of : .
- Integrate using arctan formula: Integrate using the arctan formula: .
- Substitute back for x: Substitute back for x to get the final answer: .