AI tutor
Full solution
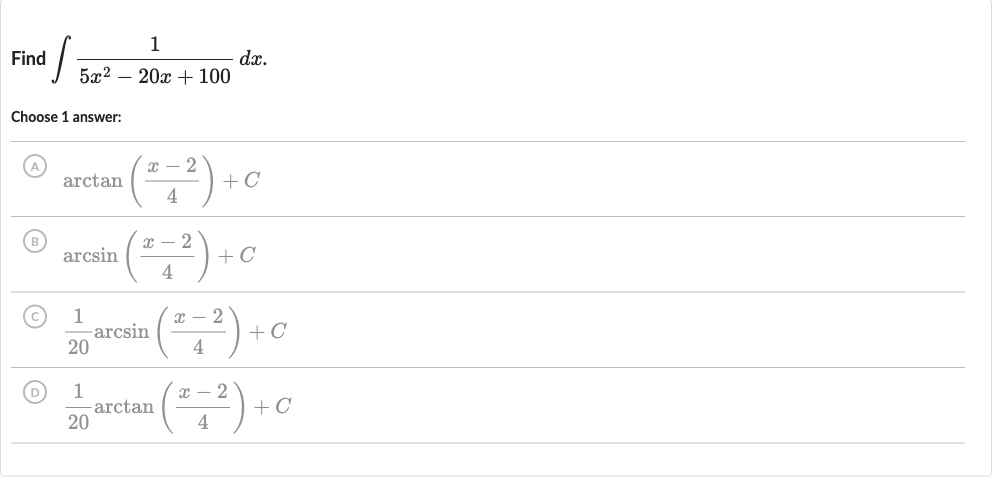
Q. Find .Choose answer:(A) (B) (c) (D)
- Rewrite Quadratic Denominator: Rewrite the quadratic in the denominator to complete the square: .
- Complete Square: Complete the square for the expression by adding and subtracting inside the parenthesis: .
- Factor Out Constant: Factor out the and rewrite the expression as .
- Standard Form Integral: Now the integral looks like , which is a standard form for the arctangent function derivative.
- Pull Out Constant: Pull out the constant from the integral: .
- Recognize Integral Form: Recognize that the integral is now in the form of , which is .
- Substitute Constants: In our case, and . So the integral becomes .
- Simplify Constants: Simplify the constants: .