AI tutor
Full solution
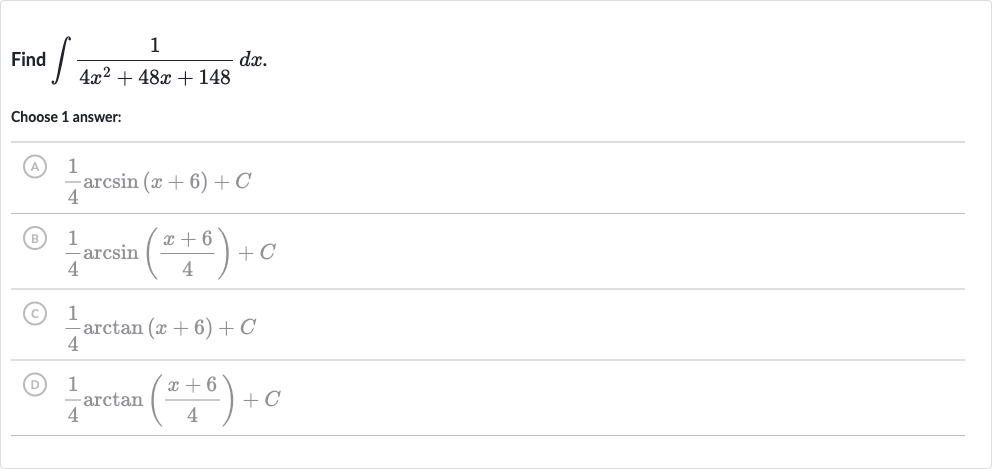
Q. Find .Choose answer:(A) (B) (C) (D)
- Complete the Square: First, complete the square for the quadratic in the denominator. can be written as .This simplifies to .
- Rewrite with Completed Square: Now, rewrite the integral with the completed square..
- Factor Out : Factor out the from the denominator to match the form of the arctan integral.
- Recognize Integral Form: Recognize that the integral is now in the form of , which is . Here, and , so .
- Calculate Integral: Calculate the integral using the arctan formula. .
- Simplify Constant: Simplify the constant in front of the arctan. simplifies to .However, this is a mistake because we should not simplify the constant yet as it is part of the standard arctan integral form.