AI tutor
Full solution
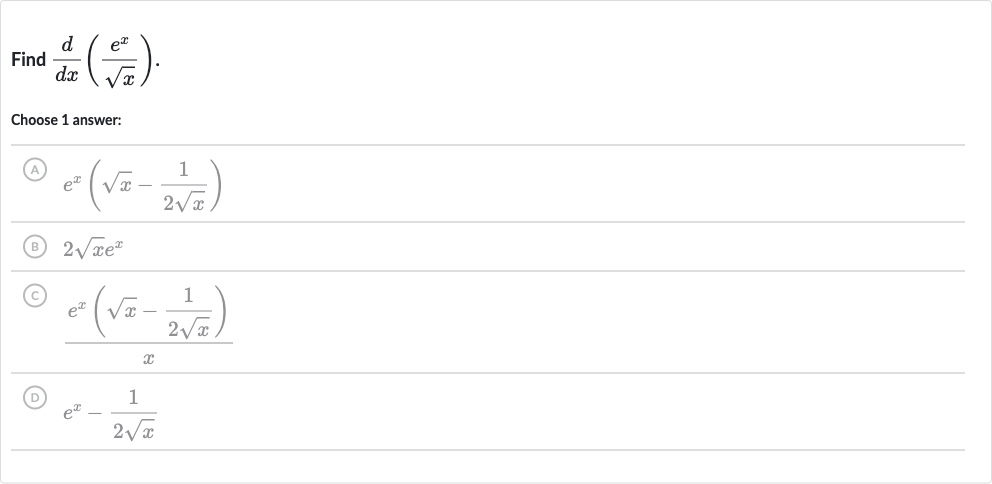
Q. Find .Choose answer:(A) (B) (C) (D)
- Apply Quotient Rule: Apply the quotient rule for differentiation, which states that the derivative of a function is given by . Let and . We need to find and .
- Find : Find the derivative of with respect to . The derivative of with respect to is . So, .
- Find : Find the derivative of with respect to . Using the power rule, , we get: .
- Apply Quotient Rule: Apply the quotient rule using the derivatives from steps and ..
- Simplify Expression: Simplify the expression. .
- Combine Terms: Combine the terms in the numerator and simplify the denominator.(\frac{d}{dx})\left(\frac{e^x}{\sqrt{x}}\right) = \frac{\frac{e^x}{\(2\)\sqrt{x}} - \frac{\(2\)e^x}{\(2\)\sqrt{x}}}{x^{\frac{\(1\)}{\(2\)}}^\(2\)}.\(\newline(\frac{d}{dx})\left(\frac{e^x}{\sqrt{x}}\right) = \frac{-\frac{e^x}{\(2\)\sqrt{x}}}{x}.
- Simplify Denominator: Simplify the complex fraction. \((\frac{d}{dx})\left(\frac{e^x}{\sqrt{x}}\right) = -\frac{e^x}{2x^{\frac{3}{2}}}.
- Simplify Complex Fraction: Notice that none of the answer choices match the simplified derivative we found. There must be a mistake in the previous steps. Let's go back and check our calculations.