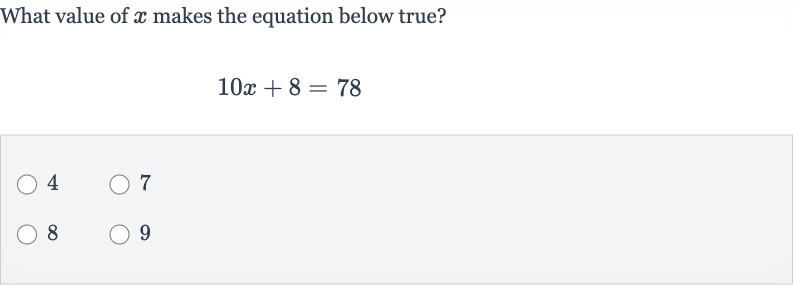AI tutor
Full solution
Q. What value of makes the equation below true?
- Write Equation: Write down the equation to solve for x.
- Subtract to Isolate: Subtract from both sides of the equation to isolate the term with .
- Divide to Solve: Divide both sides of the equation by to solve for .
More problems from Multiply two matrices
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help