Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

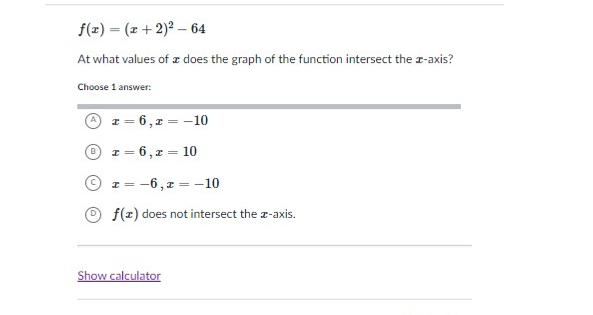
f(x)=(x+2)^(2)-64 At what values of x does the graph of the function intersect the x-axis? Choose 1 answer: (A) x=6,x=-10 (B) x=6,x=10 (C) x=-6,x=-10 D f(x) does not intersect the x-axis. Show calculator

f(x)=(x+22)^{22}−64-64 At what values of x does the graph of the function intersect the x-axis? Choose 11 answer:\newline(A) \newlinex=66,x=−10-10\newline(B) \newlinex=66,x=1010\newline(C) \newlinex=−6-6,x=−10-10\newlineD \newlinef(x) does not intersect the \newlinex-axis.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find equations of tangent lines using limitsright chevron icon

Full solution

Q. f(x)=(x+22)^{22}−64-64 At what values of x does the graph of the function intersect the x-axis? Choose 11 answer:\newline(A) \newlinex=66,x=−10-10\newline(B) \newlinex=66,x=1010\newline(C) \newlinex=−6-6,x=−10-10\newlineD \newlinef(x) does not intersect the \newlinex-axis.
  1. Set f(x)f(x) to 00: First, set f(x)f(x) to 00 because the graph intersects the xx-axis where f(x)=0f(x) = 0. 0=(x+2)2−640 = (x + 2)^2 - 64
  2. Add 6464 to isolate: Add 6464 to both sides to isolate the squared term. 64=(x+2)264 = (x + 2)^2
  3. Take square root: Take the square root of both sides to solve for x+2x + 2. 64=x+2\sqrt{64} = x + 2 8=x+28 = x + 2 or −8=x+2-8 = x + 2
  4. Solve for x: Solve for xx in both equations. x=8−2=6x = 8 - 2 = 6 x=−8−2=−10x = -8 - 2 = -10
  5. Check solutions: Check the solutions by substituting back into the original equation. For x=6x = 6: f(6)=(6+2)2−64=64−64=0f(6) = (6 + 2)^2 - 64 = 64 - 64 = 0 For x=−10x = -10: f(−10)=(−10+2)2−64=64−64=0f(-10) = (-10 + 2)^2 - 64 = 64 - 64 = 0 Both solutions are correct.

More problems from Find equations of tangent lines using limits

Question
The graphs of the functions f(x)=sin⁡(x) f(x)=\sin (x) and g(x)=12 g(x)=\frac{1}{2} intersect at 22 points on the interval 0<x<π 0<x<\pi .\newlineWhat is the area of the region bound by the graphs of f(x) f(x) and g(x) g(x) between those points of intersection ?\newlineChoose 11 answer:\newline(A) π3 \frac{\pi}{3} \newline(B) π2 \frac{\pi}{2} \newline(C) 2−π2 2-\frac{\pi}{2} \newline(D) 3−π3 \sqrt{3}-\frac{\pi}{3}
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the area of the region between the graphs of f(x)=x2+12x f(x)=x^{2}+12 x and g(x)=3x2+10 g(x)=3 x^{2}+10 from x=1 x=1 to x=4 x=4 ?\newlineChoose 11 answer:\newline(A) 7777\newline(B) 643 \frac{64}{3} \newline(C) 1818\newline(D) 4545
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the area of the region between the graphs of f(x)=x+1 f(x)=\sqrt{x+1} and g(x)=2x−4 g(x)=2 x-4 from x=0 x=0 to x=3 x=3 ?\newlineChoose 11 answer:\newline(A) 233 \frac{23}{3} \newline(B) 53 \frac{5}{3} \newline(C) 143 \frac{14}{3} \newline(D) −3-3
Get tutor helpright-arrow

Posted 9 months ago

Question
Consider the curve given by the equation 3x2+y4+6x=253 3 x^{2}+y^{4}+6 x=253 . It can be shown that dydx=−6(x+1)4y3. \frac{d y}{d x}=\frac{-6(x+1)}{4 y^{3}}. \newlineWrite the equation of the horizontal line that is tangent to the curve and is above the x x -axis.
Get tutor helpright-arrow

Posted 9 months ago

Question
The learning rate for new skills is proportional to the difference between the maximum potential for learning that skill, M M , and the amount of the skill already learned, L L .\newlineWhich equation describes this relationship?\newlineChoose 11 answer:\newline(A) L(t)=k(M−L) L(t)=\frac{k}{(M-L)} \newline(B) L(t)=k(M−L) L(t)=k(M-L) \newline(C) dLdt=k(M−L) \frac{d L}{d t}=k(M-L) \newline(D) dLdt=k(M−L) \frac{d L}{d t}=\frac{k}{(M-L)}
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the value of ddx(1x) \frac{d}{d x}\left(\frac{1}{x}\right) at x=6 x=6 ?
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the value of ddx(x) \frac{d}{d x}(\sqrt{x}) at x=9 x=9 ?
Get tutor helpright-arrow

Posted 9 months ago

Question
A curve in the plane is defined parametrically by the equations \newlinex=t3+tx=t^{3}+t and \newliney=t4+2t2y=t^{4}+2t^{2}. An equation of the line tangent to the curve at \newlinet=1t=1 is\newline(A) y=2x\text{(A)}\ y=2x\newline(B) y=8x\text{(B)}\ y=8x\newline(C) y=2x−1\text{(C)}\ y=2x-1\newline(D) y=4x−5\text{(D)}\ y=4x-5\newline(E) y=8x+13\text{(E)}\ y=8x+13
Get tutor helpright-arrow

Posted 8 months ago

Question
A pendulum is swinging next to a wall.\newlineThe distance D(t) D(t) (in cm \mathrm{cm} ) between the bob of the pendulum and the wall as a function of time t t (in seconds) can be modeled by a sinusoidal expression of the form a⋅sin⁡(b⋅t)+d a \cdot \sin (b \cdot t)+d .\newlineAt t=0 t=0 , when the pendulum is exactly in the middle of its swing, the bob is 5 cm 5 \mathrm{~cm} away from the wall. The bob reaches the closest point to the wall, which is 3 cm 3 \mathrm{~cm} from the wall, 11 second later.\newlineFind D(t) D(t) .\newlinet t should be in radians.\newlineD(t)=□ D(t)=\square
Get tutor helpright-arrow

Posted 7 months ago

Question
Pluto's distance P(t) P(t) (in billions of kilometers) from the sun as a function of time t t (in years) can be modeled by a sinusoidal expression of the form a⋅sin⁡(b⋅t)+d a \cdot \sin (b \cdot t)+d .\newlineAt year t=0 t=0 , Pluto is at its average distance from the sun, which is 66.99 billion kilometers. In 6666 years, it is at its closest point to the sun, which is 44.44 billion kilometers away.\newlineFind P(t) P(t) .\newlinet t should be in radians.\newlineP(t)= P(t)=
Get tutor helpright-arrow

Posted 7 months ago

View all (2)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant