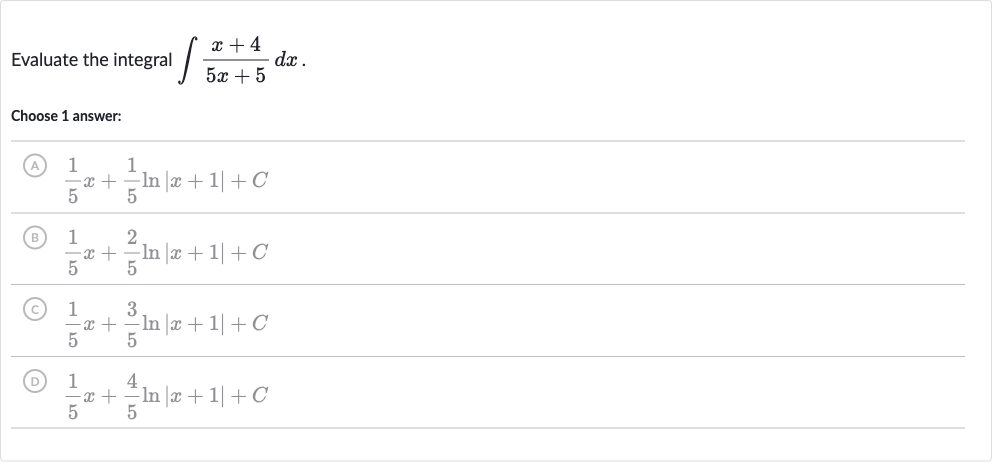
Full solution
Q. Evaluate the integral .Choose answer:(A) (B) (C) (D)
- Simplify the integrand: Simplify the integrand by factoring out the common factor in the denominator. \int\frac{x+\(4\)}{\(5\)x+\(5\)}\,dx = \int\frac{x+\(4\)}{\(5\)(x+\(1\))}\,dx
- Divide numerator by denominator: Divide each term in the numerator by the denominator.\(\newline
- Split into two integrals: Split the integral into two separate integrals.(\frac{\(1\)}{\(5\)})\int(\frac{x}{x+\(1\)} + \frac{\(4\)}{x+\(1\)})dx = (\frac{\(1\)}{\(5\)})\int(\frac{x}{x+\(1\)})dx + (\frac{\(1\)}{\(5\)})\int(\frac{\(4\)}{x+\(1\)})dx
- Recognize derivative of natural log: The first integral is the integral of \(\frac{x}{x+1}. We can simplify this by recognizing it as a derivative of a natural log.\int\left(\frac{x}{x+\(1\)}\right)dx = \ln|x+\(1| + C