AI tutor
Full solution
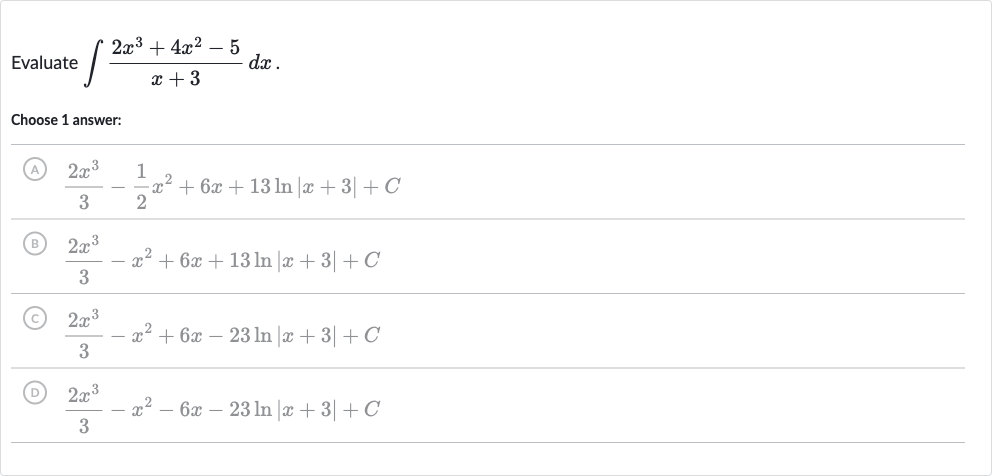
Q. Evaluate .Choose answer:(A) (B) (C) (D)
- Polynomial Long Division: First, let's try to simplify the integral by doing polynomial long division for divided by .
- Simplify Result: After dividing, we get .
- Integrate Terms Separately: Now, let's integrate each term separately: , , , and .
- Integrate : Integrating gives us .
- Integrate : Integrating gives us .
- Integrate : Integrating gives us .
- Integrate : Integrating gives us .
- Combine Integrated Parts: Adding all the integrated parts together, we get .