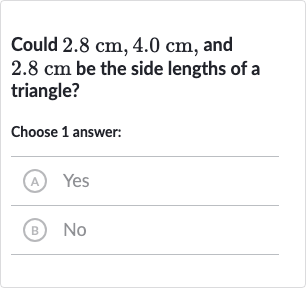
Could 2.8cm,4.0cm, and 2.8cm be the side lengths of a triangle? Choose 1 answer: (A) Yes (B) No

Question

Could  2.8cm,4.0cm, and  2.8cm be the side lengths of a triangle? Choose 1 answer: (A) Yes (B) No

Bytelearn · Accepted Answer

Triangle Inequality Theorem:  To determine if three lengths can form a triangle, we can use the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Check Shortest Sides:  We will check if the sum of the two shortest sides is greater than the longest side. The two shortest sides are 2.8cm and 2.8cm, and the longest side is 4.0cm. We calculate 2.8cm + 2.8cm > 4.0cm. Verify First Combination:  After performing the calculation, we find that 5.6cm > 4.0cm, which is true. Therefore, the lengths satisfy the Triangle Inequality Theorem for these two sides. Check Second Combination:  We must also check the other two possible combinations of sides to ensure they satisfy the Triangle Inequality Theorem. The next combination is 2.8cm (shortest side) and 4.0cm (longest side), and we check if their sum is greater than the remaining side, which is 2.8cm. We calculate 2.8cm + 4.0cm > 2.8cm. Verify Final Combination:  After performing the calculation, we find that 6.8cm > 2.8cm, which is true. Therefore, the lengths satisfy the Triangle Inequality Theorem for this combination of sides as well. Confirm Triangle Formation:  The final combination to check is the other 2.8cm side and the 4.0cm side against the remaining 2.8cm side. This is the same as the previous step and is already verified to be true.  Since all combinations of sides satisfy the Triangle Inequality Theorem, the given lengths can indeed form a triangle.

Could $2.8 \mathrm{~cm}, 4.0 \mathrm{~cm}$ , and $2.8 \mathrm{~cm}$ be the side lengths of a triangle? $\newline$ Choose $1$ answer: $\newline$ (A) Yes $\newline$ (B) No

Full solution

More problems from Is (x, y) a solution to the system of equations?

Related topics

Could 2.8 cm,4.0 cm 2.8 \mathrm{~cm}, 4.0 \mathrm{~cm} 2.8 cm,4.0 cm, and 2.8 cm 2.8 \mathrm{~cm} 2.8 cm be the side lengths of a triangle?\newlineChoose 111 answer:\newline(A) Yes\newline(B) No

Could $2.8 \mathrm{~cm}, 4.0 \mathrm{~cm}$ , and $2.8 \mathrm{~cm}$ be the side lengths of a triangle? $\newline$ Choose $1$ answer: $\newline$ (A) Yes $\newline$ (B) No