Could $10.5 \mathrm{~cm}, 8.0 \mathrm{~cm}$ , and $4.0 \mathrm{~cm}$ be the side lengths of a triangle? $\newline$ Choose $1$ answer: $\newline$ (A) Yes $\newline$ (B) No

View step-by-step help

Home

Math Problems

Algebra 2

Is (x, y) a solution to the system of equations?

Full solution

Q. Could

10.5 \mathrm{~cm}, 8.0 \mathrm{~cm}

, and

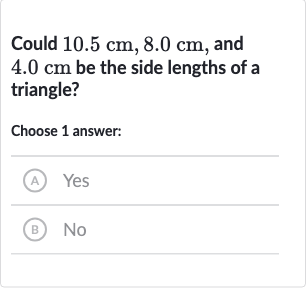
4.0 \mathrm{~cm}

be the side lengths of a triangle?

\newline

Choose

1

answer:

\newline

(A) Yes

\newline

(B) No

Check Triangle Inequality Theorem: To determine if three lengths can form a triangle, we can use the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Calculate Sum of Two Shortest Sides: First, we check if the sum of the two shortest sides is greater than the longest side. The two shortest sides are $8.0\,\text{cm}$ and $4.0\,\text{cm}$ , and the longest side is $10.5\,\text{cm}$ . We calculate $8.0\,\text{cm} + 4.0\,\text{cm}$ and compare it to $10.5\,\text{cm}$ .
Verify First Combination: The sum of the two shortest sides is $8.0\,\text{cm} + 4.0\,\text{cm} = 12.0\,\text{cm}$ , which is greater than the longest side, $10.5\,\text{cm}$ . This satisfies the Triangle Inequality Theorem for these two sides.
Verify Second Combination: Next, we check the other two combinations to ensure they also satisfy the Triangle Inequality Theorem. We check if $10.5\,\text{cm} + 4.0\,\text{cm}$ is greater than $8.0\,\text{cm}$ and if $10.5\,\text{cm} + 8.0\,\text{cm}$ is greater than $4.0\,\text{cm}$ .
Confirm Triangle Formation: The sum of $10.5\,\text{cm}$ and $4.0\,\text{cm}$ is $14.5\,\text{cm}$ , which is greater than $8.0\,\text{cm}$ . The sum of $10.5\,\text{cm}$ and $8.0\,\text{cm}$ is $18.5\,\text{cm}$ , which is greater than $4.0\,\text{cm}$ . Both of these sums satisfy the Triangle Inequality Theorem.
Confirm Triangle Formation: The sum of $10.5\,\text{cm}$ and $4.0\,\text{cm}$ is $14.5\,\text{cm}$ , which is greater than $8.0\,\text{cm}$ . The sum of $10.5\,\text{cm}$ and $8.0\,\text{cm}$ is $18.5\,\text{cm}$ , which is greater than $4.0\,\text{cm}$ . Both of these sums satisfy the Triangle Inequality Theorem. Since all three combinations of side lengths satisfy the Triangle Inequality Theorem, the lengths $10.5\,\text{cm}$ , $8.0\,\text{cm}$ , and $4.0\,\text{cm}$ can indeed form a triangle.