AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
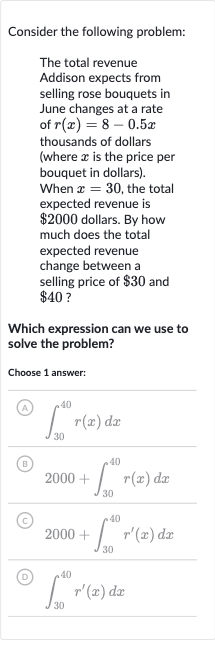
Consider the following problem:The total revenue Addison expects from selling rose bouquets in June changes at a rate of thousands of dollars (where is the price per bouquet in dollars). When , the total expected revenue is dollars. By how much does the total expected revenue change between a selling price of and ?Which expression can we use to solve the problem?Choose answer:(A) (B) (C) (D)
Full solution
Q. Consider the following problem:The total revenue Addison expects from selling rose bouquets in June changes at a rate of thousands of dollars (where is the price per bouquet in dollars). When , the total expected revenue is dollars. By how much does the total expected revenue change between a selling price of and ?Which expression can we use to solve the problem?Choose answer:(A) (B) (C) (D)
- Understand the problem: Understand the problem.We need to find the change in total expected revenue as the price per bouquet increases from to . The rate of change of revenue with respect to the price is given by the function . To find the total change in revenue, we need to integrate this rate of change over the interval from to .
- Identify the correct expression: Identify the correct expression to use.To find the total change in revenue, we integrate the rate of change function over the interval from to . The correct expression to use is the definite integral of from to , which is represented by . This corresponds to option (A).
- Evaluate the integral to find the change in revenue: Evaluate the integral to find the change in revenue.We calculate the integral of from to .The result is in thousands of dollars, so the change in revenue is .
More problems from One-step inequalities: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
