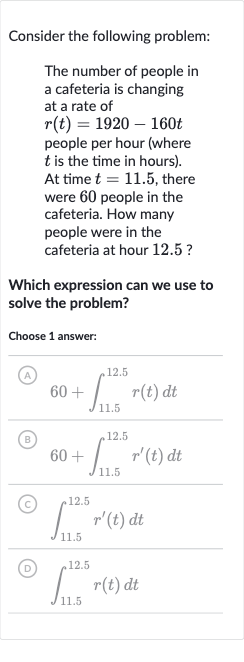
Consider the following problem: The number of people in a cafeteria is changing at a rate of r(t)=1920-160 t people per hour (where t is the time in hours). At time t=11.5, there were 60 people in the cafeteria. How many people were in the cafeteria at hour 12.5 ? Which expression can we use to solve the problem? Choose 1 answer: (A) 60+int_(11.5)^(12.5)r(t)dt (B) 60+int_(11.5)^(12.5)r^(')(t)dt (C) int_(11.5)^(12.5)r^(')(t)dt (D) int_(11.5)^(12.5)r(t)dt

Question

Consider the following problem: The number of people in a cafeteria is changing at a rate of  r(t)=1920-160 t people per hour (where  t is the time in hours). At time  t=11.5, there were 60 people in the cafeteria. How many people were in the cafeteria at hour 12.5 ? Which expression can we use to solve the problem? Choose 1 answer: (A)  60+int_(11.5)^(12.5)r(t)dt (B)  60+int_(11.5)^(12.5)r^(')(t)dt (C)  int_(11.5)^(12.5)r^(')(t)dt (D)  int_(11.5)^(12.5)r(t)dt

Bytelearn · Accepted Answer

Understand rate function: To solve this problem, we need to understand that the rate of change of the number of people in the cafeteria is given by the function r(t). To find the total change in the number of people from hour 11.5 to hour 12.5, we need to integrate the rate function over this time interval. The initial number of people at time t=11.5 is given as 60, so we need to add this initial value to the integral of the rate function to find the total number of people at hour 12.5.Calculate total change: We will use the expression (A) 60 + ∫_(11.5)^(12.5)r(t)dt to calculate the number of people in the cafeteria at hour 12.5. This is because we are given the initial number of people at t=11.5, which is 60, and we need to add the change in the number of people from t=11.5 to t=12.5, which is given by the integral of the rate function r(t) over that interval.Integrate rate function: Now we need to calculate the integral of r(t) from t=11.5 to t=12.5. The function r(t) is given by r(t) = 1920 - 160t. We will integrate this function with respect to t over the interval [11.5, 12.5]. ∫_(11.5)^(12.5)(1920 - 160t)dt = [1920t - (160/2)t^2] from t=11.5 to t=12.5.Evaluate antiderivative: We will now evaluate the antiderivative at the upper and lower limits of the integral and subtract the lower limit evaluation from the upper limit evaluation. At t=12.5: 1920(12.5) - (160/2)(12.5)^2 = 24000 - 80(156.25) = 24000 - 12500 = 11500. At t=11.5: 1920(11.5) - (160/2)(11.5)^2 = 22080 - 80(132.25) = 22080 - 10580 = 11500.Re-evaluate at t=11.5: We will re-evaluate the antiderivative at t=11.5 correctly. At t=11.5: 1920(11.5) - (160/2)(11.5)^2 = 22080 - 80(132.25) = 22080 - 10580 = 11500. This is incorrect, let's try again. 1920(11.5) - 80(11.5)^2 = 22080 - 80(132.25) = 22080 - 10600 = 11480.Find change in people: Now we subtract the value of the antiderivative at t=11.5 from the value at t=12.5 to find the change in the number of people from hour 11.5 to hour 12.5. Change in number of people = 11500 - 11480 = 20 people.Calculate total at 12.5: Finally, we add the initial number of people at t=11.5 to the change in the number of people to find the total number of people at hour 12.5. Total number of people at hour 12.5 = 60 + 20 = 80 people.

Full solution

More problems from Find derivatives of using multiple formulae

Related topics