Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Assuming
x and
y are both positive, write the following expression in simplest radical form.

sqrt(18x^(7)y^(2))
Answer:

Assuming $x$ and $y$ are both positive, write the following expression in simplest radical form. $\newline$ $\sqrt{18 x^{7} y^{2}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Simplify radical expressions with variables

Full solution

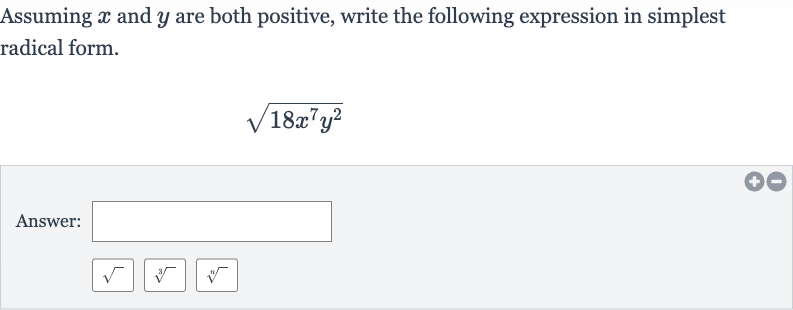
Q. Assuming

x

and

y

are both positive, write the following expression in simplest radical form.

\newline

\sqrt{18 x^{7} y^{2}}

\newline

Answer:

Factor Perfect Squares: Factor the expression inside the square root to identify perfect squares. $\sqrt{18x^{7}y^{2}}$ can be factored into $\sqrt{2 \times 3^{2} \times x^{6} \times x \times y^{2}}$ .
Separate Perfect Squares: Separate the perfect squares from the non-perfect squares inside the radical. $\newline$ We have $\sqrt{3^2 \times x^6 \times y^2 \times 2 \times x}$ which can be written as $\sqrt{3^2} \times \sqrt{x^6} \times \sqrt{y^2} \times \sqrt{2 \times x}$ .
Simplify Square Roots: Simplify the square roots of the perfect squares. Since $\sqrt{3^2} = 3$ , $\sqrt{x^6} = x^3$ , and $\sqrt{y^2} = y$ , we have $3 \times x^3 \times y \times \sqrt{2 \times x}$ .
Combine Simplified Terms: Combine the simplified terms. $\newline$ The expression simplifies to $3x^3y \cdot \sqrt{2x}$ .
Check Simplified Form: Check if the simplified expression is in its simplest radical form. $\newline$ Since $2x$ does not have any perfect square factors other than $1$ , and $x$ is assumed to be positive, the expression $3x^3y \times \sqrt{2x}$ is indeed in its simplest radical form.

More problems from Simplify radical expressions with variables

Question

\newline

500

=

Posted 9 months ago

Question

\newline

2,000

=

Posted 9 months ago

Question

\newline

750

=

Posted 9 months ago

Question

\newline

1,500

=

Posted 9 months ago

Question

\newline

1,500

=

Posted 9 months ago

Question

According to Newton's Second Law of Motion, the sum of the forces that act on an object with a mass

m

that moves with an acceleration

a

m \cdot a

. An object whose mass is

80

grams has an acceleration of

20

meters per seconds squared. What calculation will give us the sum of the forces that act on the object, in Newtons (which are

\frac{\text{kg} \cdot \text{m}}{\text{s}^2}

\newline

1

\newline

80 \cdot 20

\newline

80 \cdot 1000 \cdot 20

\newline

\frac{80}{1000} \cdot 20

\newline

\frac{80}{60^2} \cdot 20

Posted 8 months ago

Question

\newline

Multiply and remove all perfect squares from inside the square roots. Assume

\newline

b

\newline

2\sqrt{8b^{3}} \cdot 9\sqrt{18b} =

Posted 10 months ago

Question

Roselyn is driving to visit her family, who live

150

kilometers away. Her average speed is

60

kilometers per hour. The car's tank has

20

liters of fuel at the beginning of the drive, and its fuel efficiency is

6

kilometers per liter. Fuel costs

0.60

dollars per liter.

\newline

How long can Roselyn drive before she runs out of fuel?

\newline

Posted 10 months ago

Question

Astrid is in charge of building a new fleet of ships. Each ship requires

40

tons of wood, and accommodates

300

sailors. She receives a delivery of

4

tons of wood each day. The deliveries can continue for

100

days at most, afterwards the weather is too bad to allow them. Overall, she wants to build enough ships to accommodate at least

2100

\newline

How much wood does Astrid need to accommodate

2100

\newline

Posted 10 months ago

Question

Lily's car has a fuel efficiency of

8 \text{ liters}

100 \text{ kilometers}

\newline

What is the fuel efficiency of Lily's car in

\text{kilometers}

\text{liter}

\newline

\frac{\text{km}}{\text{L}}

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant