Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the zeros of the function. Enter the solutions from least to greatest. f(x)=(x-4)^(2)-25 lesser x= greater x=

Find the zeros of the function. Enter the solutions from least to greatest.\newlinef(x)=(x−4)2−25 f(x)=(x-4)^{2}-25 \newlinelesser x= x= \newlinegreater x= x=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of absolute value functions: translations and reflectionsright chevron icon

Full solution

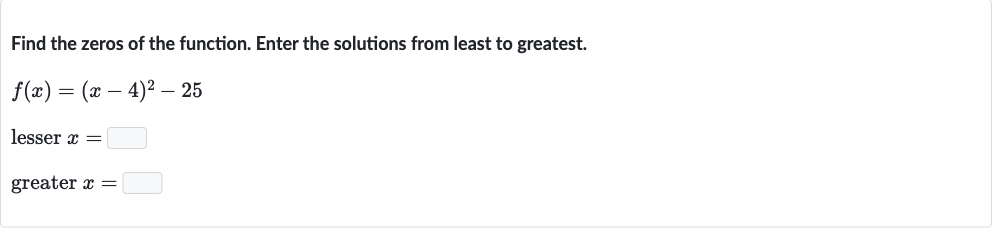
Q. Find the zeros of the function. Enter the solutions from least to greatest.\newlinef(x)=(x−4)2−25 f(x)=(x-4)^{2}-25 \newlinelesser x= x= \newlinegreater x= x=
  1. Find zeros of the function: Set the function equal to zero to find its zeros.\newlinef(x)=(x−4)2−25=0f(x) = (x - 4)^2 - 25 = 0
  2. Solve the quadratic equation: Solve the quadratic equation.\newline(x−4)2−25=0(x - 4)^2 - 25 = 0\newlineAdd 2525 to both sides to isolate the squared term.\newline(x−4)2=25(x - 4)^2 = 25
  3. Isolate the squared term: Take the square root of both sides.\newline(x−4)2=±25\sqrt{(x - 4)^2} = \pm\sqrt{25}\newlinex−4=±5x - 4 = \pm5
  4. Take the square root: Solve for x by adding 44 to both sides of the equation.\newlineFor the positive root:\newlinex−4+4=5+4x - 4 + 4 = 5 + 4\newlinex=9x = 9\newlineFor the negative root:\newlinex−4+4=−5+4x - 4 + 4 = -5 + 4\newlinex=−1x = -1
  5. Solve for x: Write the solutions in ascending order.\newlinelesser x=−1x = -1\newlinegreater x=9x = 9

More problems from Transformations of absolute value functions: translations and reflections

Question
Find g(x) g(x) , where g(x) g(x) is the translation 2 2 units left of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the reflection across the y y -axis of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 77 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=7∣x∣ y=7|x| \newline(B) y=−7∣x∣ y=-7|x| \newlineC) y=17∣x∣ y=\frac{1}{7}|x| \newline(D) y=−17∣x∣ y=-\frac{1}{7}|x|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 66 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x−6∣ y=|x-6| \newline(B) y=6∣x∣ y=6|x| \newline(C) y=16∣x∣ y=\frac{1}{6}|x| \newline(D) y=∣x−16∣ y=\left|x-\frac{1}{6}\right|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 13 \frac{1}{3} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−3 y=|x|-3 \newline(B) y=−3∣x∣ y=-3|x| \newline(C) y=13∣x∣ y=\frac{1}{3}|x| \newline(D) y=∣x∣−13 y=|x|-\frac{1}{3}
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted to the left by 66 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x+6∣−6 y=|x+6|-6 \newline(B) y=∣x−6∣−6 y=|x-6|-6 \newline(C) y=∣x∣−6 y=|x|-6 \newline(D) y=∣x+6∣ y=|x+6|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 14 \frac{1}{4} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=−4∣x∣ y=-4|x| \newline(B) y=∣x∣−4 y=|x|-4 \newline(C) y=−14∣x∣ y=-\frac{1}{4}|x| \newline(D) y=∣x−4∣ y=|x-4|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted down by 99 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−9 y=|x|-9 \newline(B) y=∣x+9∣ y=|x+9| \newline(C) y=∣x∣+9 y=|x|+9 \newline(D) y=∣x−9∣ y=|x-9|
Get tutor helpright-arrow

Posted 10 months ago

Question
y=13x+5y=2x \begin{array}{l} y=\frac{1}{3} x+5 \\ y=2 x \end{array} \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of y+x y+x ?
Get tutor helpright-arrow

Posted 3 months ago

Question
13x+3y=4 \frac{1}{3} x+3 y=4 \newline2x−4=2y 2 x-4=2 y \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of x−y x-y ?
Get tutor helpright-arrow

Posted 2 months ago

View all (49)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant