Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(x-4)(x-5)=0 If x=s and x=t are the solutions to the given equation, which of the following is equal to the value of |s-t| ? Choose 1 answer: (A) -9 (B) -1 (c) 1 (D) 9

(x−4)(x−5)=0 (x-4)(x-5)=0 \newlineIf x=s x=s and x=t x=t are the solutions to the given equation, which of the following is equal to the value of ∣s−t∣ |s-t| ?\newlineChoose 11 answer:\newline(A) −9-9\newline(B) −1-1\newline(C) 11\newline(D) 99

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of absolute value functions: translations and reflectionsright chevron icon

Full solution

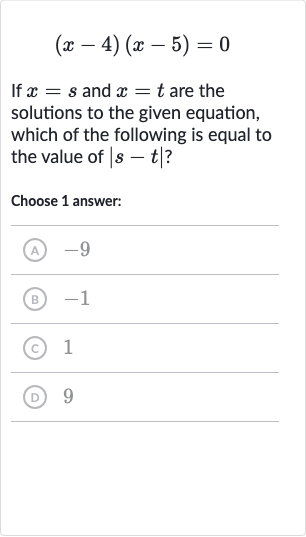
Q. (x−4)(x−5)=0 (x-4)(x-5)=0 \newlineIf x=s x=s and x=t x=t are the solutions to the given equation, which of the following is equal to the value of ∣s−t∣ |s-t| ?\newlineChoose 11 answer:\newline(A) −9-9\newline(B) −1-1\newline(C) 11\newline(D) 99
  1. Find Solutions: We need to find the solutions to the equation (x−4)(x−5)=0(x-4)(x-5)=0.\newlineThe equation is already factored, so we can use the zero product property, which states that if a product of two factors is zero, then at least one of the factors must be zero.\newlineSetting each factor equal to zero gives us two equations:\newline11. x−4=0x - 4 = 0\newline22. x−5=0x - 5 = 0
  2. Apply Zero Product Property: Solve the first equation x−4=0x - 4 = 0 for xx.\newlineAdding 44 to both sides of the equation gives us:\newlinex=4x = 4\newlineThis is our first solution, so we can say s=4s = 4.
  3. Solve Equation 11: Solve the second equation x−5=0x - 5 = 0 for xx.\newlineAdding 55 to both sides of the equation gives us:\newlinex=5x = 5\newlineThis is our second solution, so we can say t=5t = 5.
  4. Solve Equation 22: Now we need to find the absolute value of the difference between ss and tt, which is ∣s−t∣|s-t|.\newlineSubstitute s=4s = 4 and t=5t = 5 into the expression ∣s−t∣|s-t|:\newline∣s−t∣=∣4−5∣|s-t| = |4-5|
  5. Calculate Absolute Difference: Calculate the value of ∣4−5∣|4-5|.\newline∣4−5∣=∣−1∣|4-5| = |-1|\newlineThe absolute value of −1-1 is 11, so ∣4−5∣=1|4-5| = 1.

More problems from Transformations of absolute value functions: translations and reflections

Question
Find g(x) g(x) , where g(x) g(x) is the translation 2 2 units left of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the reflection across the y y -axis of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 77 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=7∣x∣ y=7|x| \newline(B) y=−7∣x∣ y=-7|x| \newlineC) y=17∣x∣ y=\frac{1}{7}|x| \newline(D) y=−17∣x∣ y=-\frac{1}{7}|x|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 66 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x−6∣ y=|x-6| \newline(B) y=6∣x∣ y=6|x| \newline(C) y=16∣x∣ y=\frac{1}{6}|x| \newline(D) y=∣x−16∣ y=\left|x-\frac{1}{6}\right|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 13 \frac{1}{3} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−3 y=|x|-3 \newline(B) y=−3∣x∣ y=-3|x| \newline(C) y=13∣x∣ y=\frac{1}{3}|x| \newline(D) y=∣x∣−13 y=|x|-\frac{1}{3}
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted to the left by 66 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x+6∣−6 y=|x+6|-6 \newline(B) y=∣x−6∣−6 y=|x-6|-6 \newline(C) y=∣x∣−6 y=|x|-6 \newline(D) y=∣x+6∣ y=|x+6|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 14 \frac{1}{4} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=−4∣x∣ y=-4|x| \newline(B) y=∣x∣−4 y=|x|-4 \newline(C) y=−14∣x∣ y=-\frac{1}{4}|x| \newline(D) y=∣x−4∣ y=|x-4|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted down by 99 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−9 y=|x|-9 \newline(B) y=∣x+9∣ y=|x+9| \newline(C) y=∣x∣+9 y=|x|+9 \newline(D) y=∣x−9∣ y=|x-9|
Get tutor helpright-arrow

Posted 10 months ago

Question
y=13x+5y=2x \begin{array}{l} y=\frac{1}{3} x+5 \\ y=2 x \end{array} \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of y+x y+x ?
Get tutor helpright-arrow

Posted 3 months ago

Question
13x+3y=4 \frac{1}{3} x+3 y=4 \newline2x−4=2y 2 x-4=2 y \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of x−y x-y ?
Get tutor helpright-arrow

Posted 2 months ago

View all (49)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant