Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(3y-2)(y+a)=3y^(2)+bz If the given equation is true for all values of y, where a and b are constants, which of the following is the value of b ? Choose 1 answer: (A) -38 (B) 12 (c) 34 (D) 36

(3y−2)(y+a)=3y2+bz (3 y-2)(y+a)=3 y^{2}+b z \newlineIf the given equation is true for all values of y y , where a a and b b are constants, which of the following is the value of b b ?\newlineChoose 11 answer:\newline(A) −38-38\newline(B) 1212\newline(C) 3434\newline(D) 3636

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of absolute value functions: translations and reflectionsright chevron icon

Full solution

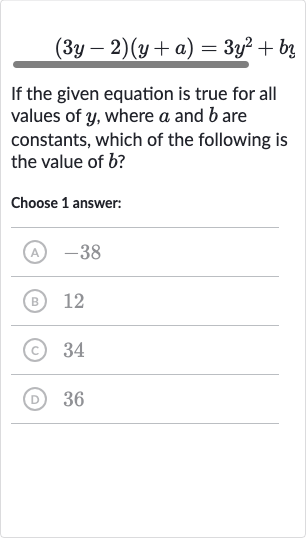
Q. (3y−2)(y+a)=3y2+bz (3 y-2)(y+a)=3 y^{2}+b z \newlineIf the given equation is true for all values of y y , where a a and b b are constants, which of the following is the value of b b ?\newlineChoose 11 answer:\newline(A) −38-38\newline(B) 1212\newline(C) 3434\newline(D) 3636
  1. Expand and Compare: We need to expand the left side of the equation (3y−2)(y+a)(3y-2)(y+a) to compare it with the right side 3y2+bz3y^2+bz.(3y−2)(y+a)=3y(y)+3y(a)−2(y)−2(a)(3y-2)(y+a) = 3y(y) + 3y(a) - 2(y) - 2(a)
  2. Simplify Expression: Now we simplify the expression by multiplying the terms.\newline3y(y)+3y(a)−2(y)−2(a)=3y2+3ay−2y−2a3y(y) + 3y(a) - 2(y) - 2(a) = 3y^2 + 3ay - 2y - 2a
  3. Comparison with Right Side: We compare the simplified expression with the right side of the given equation.\newline3y2+3ay−2y−2a=3y2+bz3y^2 + 3ay - 2y - 2a = 3y^2 + bz
  4. Coefficient Comparison for yy: Since the equation is true for all values of yy, the coefficients of the corresponding terms on both sides must be equal. This means that the coefficient of yy on the left side (3a−2)(3a - 2) must be equal to the coefficient of yy on the right side, which is 00 (since there is no yy term on the right side).\newline3a−2=03a - 2 = 0
  5. Solve for aa: We solve for aa.3a−2=03a - 2 = 03a=23a = 2a=23a = \frac{2}{3}
  6. Constant Term Comparison: Now we look for the constant term on the left side, which is −2a-2a, and compare it with the constant term on the right side, which is bzbz. \newline−2a=bz-2a = bz
  7. Substitute Value of a: We substitute the value of aa into the equation.−2(23)=bz-2\left(\frac{2}{3}\right) = bz−43=bz-\frac{4}{3} = bz
  8. Determine Coefficient for bb: Since there is no zz term on the left side of the original equation, the coefficient of zz on the right side must be 00. Therefore, bb must be 00.
    bz=0bz = 0
    b=0b = 0

More problems from Transformations of absolute value functions: translations and reflections

Question
Find g(x) g(x) , where g(x) g(x) is the translation 2 2 units left of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the reflection across the y y -axis of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 77 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=7∣x∣ y=7|x| \newline(B) y=−7∣x∣ y=-7|x| \newlineC) y=17∣x∣ y=\frac{1}{7}|x| \newline(D) y=−17∣x∣ y=-\frac{1}{7}|x|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 66 .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x−6∣ y=|x-6| \newline(B) y=6∣x∣ y=6|x| \newline(C) y=16∣x∣ y=\frac{1}{6}|x| \newline(D) y=∣x−16∣ y=\left|x-\frac{1}{6}\right|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is scaled vertically by a factor of 13 \frac{1}{3} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−3 y=|x|-3 \newline(B) y=−3∣x∣ y=-3|x| \newline(C) y=13∣x∣ y=\frac{1}{3}|x| \newline(D) y=∣x∣−13 y=|x|-\frac{1}{3}
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted to the left by 66 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x+6∣−6 y=|x+6|-6 \newline(B) y=∣x−6∣−6 y=|x-6|-6 \newline(C) y=∣x∣−6 y=|x|-6 \newline(D) y=∣x+6∣ y=|x+6|
Get tutor helpright-arrow

Posted 7 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 14 \frac{1}{4} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=−4∣x∣ y=-4|x| \newline(B) y=∣x∣−4 y=|x|-4 \newline(C) y=−14∣x∣ y=-\frac{1}{4}|x| \newline(D) y=∣x−4∣ y=|x-4|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is shifted down by 99 units.\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=∣x∣−9 y=|x|-9 \newline(B) y=∣x+9∣ y=|x+9| \newline(C) y=∣x∣+9 y=|x|+9 \newline(D) y=∣x−9∣ y=|x-9|
Get tutor helpright-arrow

Posted 10 months ago

Question
y=13x+5y=2x \begin{array}{l} y=\frac{1}{3} x+5 \\ y=2 x \end{array} \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of y+x y+x ?
Get tutor helpright-arrow

Posted 3 months ago

Question
13x+3y=4 \frac{1}{3} x+3 y=4 \newline2x−4=2y 2 x-4=2 y \newlineConsider the given system of equations. If (x,y) (x, y) is the solution to the system, then what is the value of x−y x-y ?
Get tutor helpright-arrow

Posted 2 months ago

View all (49)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant