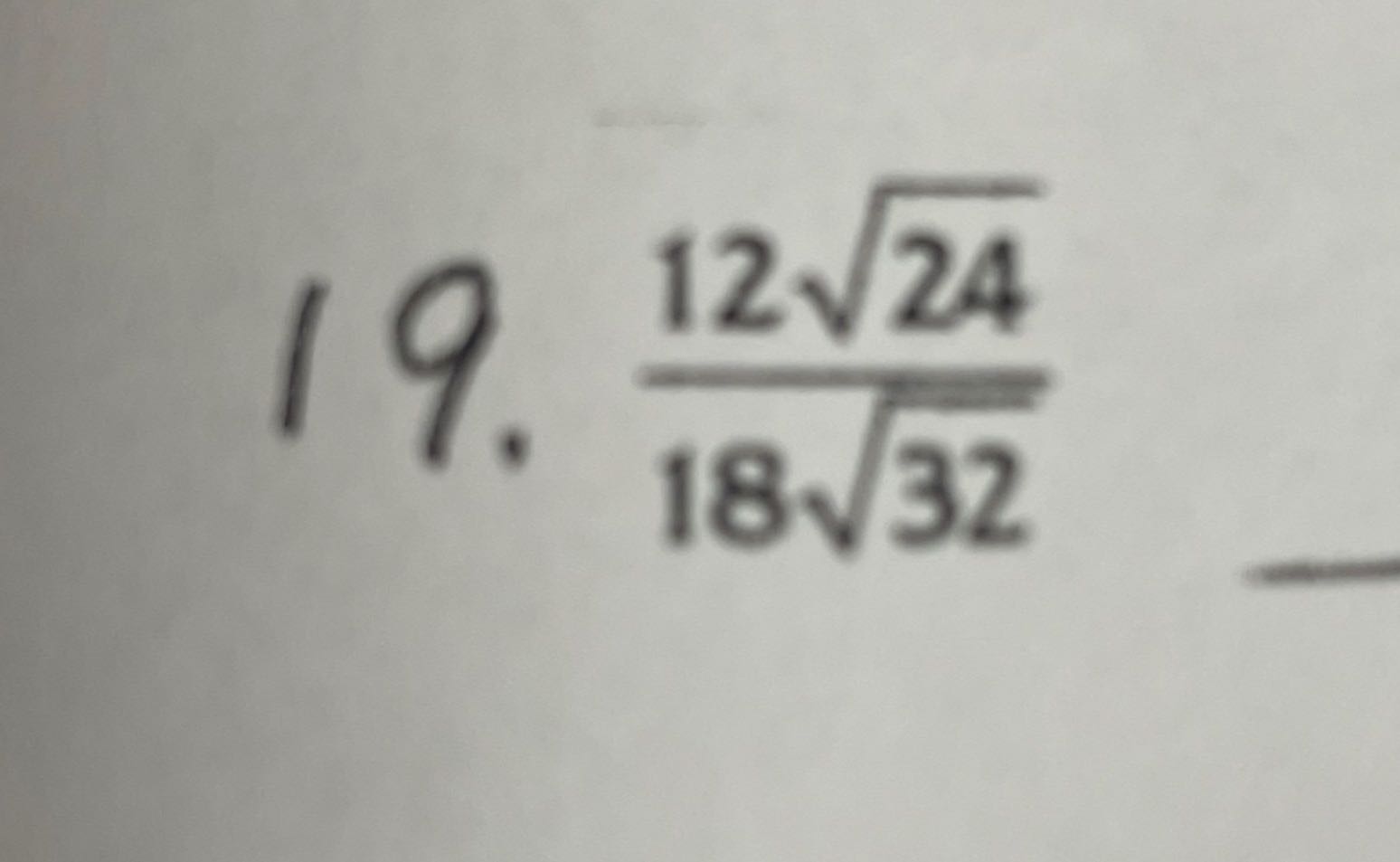Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(12sqrt24)/(18sqrt32)=

$\frac{12 \sqrt{24}}{18 \sqrt{32}}$ =

View step-by-step help

View step-by-step help

Simplify radical expressions involving fractions

Full solution

Q.

\frac{12 \sqrt{24}}{18 \sqrt{32}}

=

Apply Quotient Rule of Radicals: Apply the quotient rule of radicals to simplify the expression. $\newline$ $(12\sqrt{24})/(18\sqrt{32}) = (12/18) \times (\sqrt{24}/\sqrt{32})$
Simplify Fraction $12$ / $18$ : Simplify the fraction $\frac{12}{18}$ by dividing both numerator and denominator by their greatest common divisor, which is $6$ . $\left(\frac{12}{18}\right) = \frac{12 \div 6}{18 \div 6} = \frac{2}{3}$
Find Prime Factorization: Simplify the radical expression $\sqrt{24}/\sqrt{32}$ by finding the prime factorization of the numbers under the radicals. $\newline$ $\sqrt{24} = \sqrt{(2 \times 2 \times 2 \times 3)} = \sqrt{2^3 \times 3}$ $\newline$ $\sqrt{32} = \sqrt{(2 \times 2 \times 2 \times 2 \times 2)} = \sqrt{2^5}$
Take Out Pairs of Prime Factors: Simplify the radicals by taking out pairs of prime factors. $\newline$ $\sqrt{24} = \sqrt{2^3 \times 3} = 2\sqrt{2 \times 3} = 2\sqrt{6}$ $\newline$ $\sqrt{32} = \sqrt{2^5} = 2^2\sqrt{2} = 4\sqrt{2}$
Substitute Simplified Radicals: Now, substitute the simplified radicals back into the expression. $(\frac{2}{3}) \times (\frac{2\sqrt{6}}{4\sqrt{2}})$
Divide Coefficients and Radicals: Simplify the expression by dividing the coefficients $\frac{2}{4}$ and the radicals $\frac{\sqrt{6}}{\sqrt{2}}$ . $\frac{2}{4} = \frac{1}{2}$ $\frac{\sqrt{6}}{\sqrt{2}} = \sqrt{\frac{6}{2}} = \sqrt{3}$
Combine Coefficients and Radicals: Combine the simplified coefficients and radicals. $\newline$ $(\frac{1}{2}) \times (\frac{2}{3}) \times \sqrt{3} = (\frac{2}{6}) \times \sqrt{3} = (\frac{1}{3}) \times \sqrt{3}$
Final Simplified Form: The final simplified form of the expression is $(\frac{1}{3}) \times \sqrt{3}$ .

More problems from Simplify radical expressions involving fractions

Question

\newline

\sqrt{\frac{9}{25}}

\newline

Posted 2 months ago

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 2 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 2 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 2 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 2 months ago

Question

\newline

500

=

Posted 3 months ago

Question

\newline

2,000

=

Posted 3 months ago

Question

\newline

750

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago