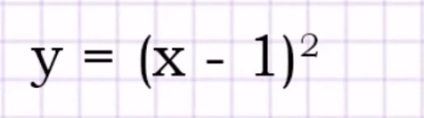Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Differentiate: y=(x-1)^(2)

Differentiate: y=(x−1)2y=(x-1)^{2}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find derivatives using the chain rule IIright chevron icon

Full solution

Q. Differentiate: y=(x−1)2y=(x-1)^{2}
  1. Identify Function and Rule: Identify the function and the rule needed for differentiation.\newlineWe have y=(x−1)2y = (x-1)^2, which is a basic power function.\newlineUsing the power rule for differentiation, where if y=uny = u^n, then y′=n⋅u(n−1)⋅u′y' = n\cdot u^{(n-1)}\cdot u'.
  2. Differentiate Inside Function: Differentiate the inside function u=x−1u = x-1. Differentiating u=x−1u = x-1 gives us u′=1u' = 1.
  3. Apply Chain Rule: Apply the chain rule.\newlineUsing the power rule and the result from the previous step, the derivative y′=2⋅(x−1)2−1⋅1y' = 2\cdot(x-1)^{2-1}\cdot1.\newlineSimplify to get y′=2⋅(x−1)y' = 2\cdot(x-1).

More problems from Find derivatives using the chain rule II

Question
Find the derivative of f(x) f(x) .\newlinef(x)=cos⁡(x) f(x) = \cos(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡(x) f(x) = \tan(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ex f(x) = e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ln⁡(x) f(x) = \ln(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡−1x f(x) = \tan^{-1}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=xex f(x) = x e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=exx f(x) = \frac{e^x}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of f(x) f(x) . \newline f(x)=e(x+1) f(x) = e^{(x + 1)} \newline f′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=x+3 f(x) = \sqrt{x+3} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Find the derivative of g(x) g(x). \newline g(x)=ln⁡(2x) g(x) = \ln(2x) \newline g′(x)= g^{\prime}(x) = ______
Get tutor helpright-arrow

Posted 9 months ago

View all (13)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant