Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

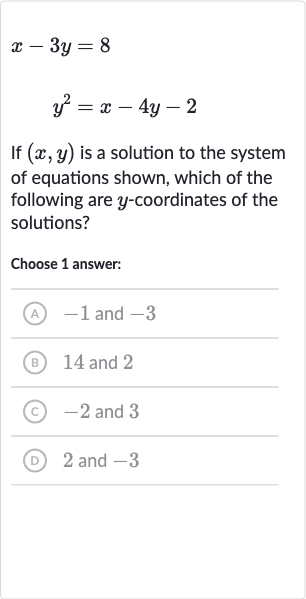
x-3y=8

y^(2)=x-4y-2
If
(x,y) is a solution to the system of equations shown, which of the following are
y-coordinates of the solutions?
Choose 1 answer:
(A) -1 and -3
(B) 14 and 2
(C) -2 and 3
(D) 2 and -3

$x-3 y=8$ $\newline$ $y^{2}=x-4 y-2$ $\newline$ If $(x, y)$ is a solution to the system of equations shown, which of the following are $y$ -coordinates of the solutions? $\newline$ Choose $1$ answer: $\newline$ (A) $-1$ and $-3$ $\newline$ (B) $14$ and $2$ $\newline$ (C) $-2$ and $3$ $\newline$ (D) $2$ and $-3$

View step-by-step help

View step-by-step help

Mean, median, mode, and range: find the missing number

Full solution

Q.

x-3 y=8

\newline

y^{2}=x-4 y-2

\newline

If

(x, y)

is a solution to the system of equations shown, which of the following are

y

-coordinates of the solutions?

\newline

Choose

1

answer:

\newline

(A)

-1

and

-3

\newline

(B)

14

and

2

\newline

(C)

-2

and

3

\newline

(D)

2

and

-3

Solve for x: Solve the first equation for x. $\newline$ The first equation is $x - 3y = 8$ . To solve for x, add $3y$ to both sides of the equation. $\newline$ $x = 3y + 8$
Substitute into second equation: Substitute the expression for $x$ into the second equation. $\newline$ The second equation is $y^2 = x - 4y - 2$ . Substitute $x$ with $3y + 8$ . $\newline$ $y^2 = (3y + 8) - 4y - 2$
Simplify the equation: Simplify the equation. $\newline$ Combine like terms on the right side of the equation. $\newline$ $y^2 = 3y + 8 - 4y - 2$ $\newline$ $y^2 = -y + 6$
Rearrange for quadratic equation: Rearrange the equation to form a quadratic equation. $\newline$ Add $y$ to both sides and subtract $6$ from both sides to set the equation to zero. $\newline$ $y^2 + y - 6 = 0$
Factor the quadratic equation: Factor the quadratic equation. $\newline$ We need to find two numbers that multiply to $-6$ and add up to $1$ . These numbers are $3$ and $-2$ . $\newline$ $(y + 3)(y - 2) = 0$
Solve for y: Solve for y. $\newline$ Set each factor equal to zero and solve for y. $\newline$ $y + 3 = 0$ or $y - 2 = 0$ $\newline$ $y = -3$ or $y = 2$

More problems from Mean, median, mode, and range: find the missing number

Question

In the data set below, what is the mean absolute deviation?

\newline

6,3,1,6,6

\newline

If the answer is a decimal, round it to the nearest tenth.

\newline

mean absolute deviation (MAD): _____

Posted 2 months ago

Question

Look at this set of

8

60, 38, 93, 14, 23, 81, 12, 64

, How would the range change if the number

18

replaced the number

12

\newline

\newline

\newline

\newline

Posted 1 month ago

Question

Liam has the following data:

20,7,x,20

. If the mean is

14

, which number could

x

\newline

\newline

(A)9

\newline

(B)21

Posted 2 months ago

Question

g=15-\frac{m}{32}

\newline

If Vera starts with a full tank of gas, the number of gallons of gas,

g

, left in the tank after driving

m

miles is given by the equation. When full, how many gallons of gas does Vera's tank hold?

\newline

1

\newline

15

\newline

17

\newline

32

\newline

480

Posted 4 months ago

Question

Which of the following expressions is equivalent to

-2 x y+18

\newline

1

\newline

-2(x y-9)

\newline

-2(x y+9)

\newline

2(x y-9)

\newline

2(x y+9)

Posted 1 month ago

Question

What is the value of

\tan \left(\frac{\pi}{3}\right)

\newline

1

\newline

\frac{1}{2}

\newline

\frac{\sqrt{3}}{3}

\newline

\frac{\sqrt{3}}{2}

\newline

\sqrt{3}

Posted 4 months ago

Question

Which of the following is the value of

\tan (\pi)

\newline

1

\newline

1

\newline

0

\newline

-1

\newline

\tan (\pi)

Posted 4 months ago

Question

Which of the following is the value of

\sin \left(\frac{\pi}{2}\right) ?

\newline

1

\newline

-1

\newline

0

\newline

\frac{\sqrt{2}}{2}

\newline

1

Posted 4 months ago

Question

\begin{array}{l} 3 x+y=3 \\ 7 x-y=2 \end{array}

\newline

The given system of equations has solution

(x, y)

. What is the value of

x

Posted 1 month ago

Question

56x8

Posted 8 hours ago