Full solution
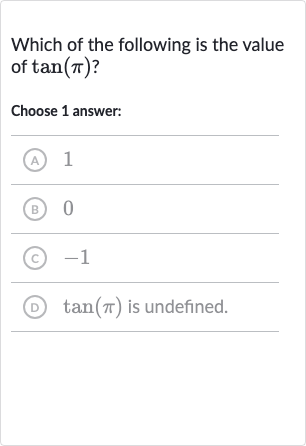
Q. Which of the following is the value of ?Choose answer:(A) (B) (C) (D) is undefined.
- Understanding the Unit Circle: To find the value of , we need to understand the unit circle and the definition of the tangent function. The tangent of an angle in the unit circle is the ratio of the y-coordinate to the x-coordinate of the point on the unit circle at that angle, provided the x-coordinate is not zero. For the angle , the point on the unit circle is .
- Calculating : Since the tangent function is the ratio of the y-coordinate to the x-coordinate, we calculate as follows:
- Defining the Tangent Function: We must also remember that the tangent function is defined for all real numbers except for odd multiples of , where the cosine function is zero and the tangent function is undefined. Since is not an odd multiple of , is defined.
- Value of : Therefore, the value of is , which corresponds to choice (B).
More problems from Mean, median, mode, and range: find the missing number
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help