Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the value of
tan((pi)/(3)) ?
Choose 1 answer:
(A)
(1)/(2)
(B)
(sqrt3)/(3)
(c)
(sqrt3)/(2)
(D)
sqrt3

What is the value of $\tan \left(\frac{\pi}{3}\right)$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{1}{2}$ $\newline$ (B) $\frac{\sqrt{3}}{3}$ $\newline$ (C) $\frac{\sqrt{3}}{2}$ $\newline$ (D) $\sqrt{3}$

View step-by-step help

View step-by-step help

Mean, median, mode, and range: find the missing number

Full solution

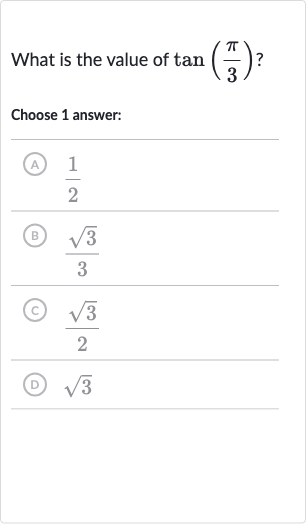
Q. What is the value of

\tan \left(\frac{\pi}{3}\right)

?

\newline

Choose

1

answer:

\newline

(A)

\frac{1}{2}

\newline

(B)

\frac{\sqrt{3}}{3}

\newline

(C)

\frac{\sqrt{3}}{2}

\newline

(D)

\sqrt{3}

Recalling the unit circle: To find the value of $\tan\left(\frac{\pi}{3}\right)$ , we need to recall the unit circle or the special triangles. The angle $\frac{\pi}{3}$ radians corresponds to $60$ degrees.
Using a $30$ $-60$ $-90$ triangle: In a $30$ $-60$ $-90$ right triangle, the sides are in the ratio $1 : \sqrt{3} : 2$ . The shortest side (opposite the $30$ -degree angle) is $1$ , the side opposite the $60$ -degree angle (which is $\tan\left(\frac{\pi}{3}\right)$ ) is $\sqrt{3}$ , and the hypotenuse (opposite the $90$ -degree angle) is $2$ .
Finding the tangent of $\frac{\pi}{3}$ : The tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side. So, $\tan\left(\frac{\pi}{3}\right) = \frac{\text{length of opposite side to } 60^\circ}{\text{length of adjacent side to } 60^\circ}$ .
Applying the side ratios: Using the side ratios for a $30$ $-60$ $-90$ triangle, $\tan\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{1} = \sqrt{3}$ .

More problems from Mean, median, mode, and range: find the missing number

Question

In the data set below, what is the mean absolute deviation?

\newline

6,3,1,6,6

\newline

If the answer is a decimal, round it to the nearest tenth.

\newline

mean absolute deviation (MAD): _____

Posted 2 months ago

Question

Look at this set of

8

60, 38, 93, 14, 23, 81, 12, 64

, How would the range change if the number

18

replaced the number

12

\newline

\newline

\newline

\newline

Posted 1 month ago

Question

Liam has the following data:

20,7,x,20

. If the mean is

14

, which number could

x

\newline

\newline

(A)9

\newline

(B)21

Posted 2 months ago

Question

g=15-\frac{m}{32}

\newline

If Vera starts with a full tank of gas, the number of gallons of gas,

g

, left in the tank after driving

m

miles is given by the equation. When full, how many gallons of gas does Vera's tank hold?

\newline

1

\newline

15

\newline

17

\newline

32

\newline

480

Posted 4 months ago

Question

x-3 y=8

\newline

y^{2}=x-4 y-2

\newline

(x, y)

is a solution to the system of equations shown, which of the following are

y

-coordinates of the solutions?

\newline

1

\newline

-1

-3

\newline

14

2

\newline

-2

3

\newline

2

-3

Posted 2 months ago

Question

Which of the following expressions is equivalent to

-2 x y+18

\newline

1

\newline

-2(x y-9)

\newline

-2(x y+9)

\newline

2(x y-9)

\newline

2(x y+9)

Posted 1 month ago

Question

Which of the following is the value of

\tan (\pi)

\newline

1

\newline

1

\newline

0

\newline

-1

\newline

\tan (\pi)

Posted 4 months ago

Question

Which of the following is the value of

\sin \left(\frac{\pi}{2}\right) ?

\newline

1

\newline

-1

\newline

0

\newline

\frac{\sqrt{2}}{2}

\newline

1

Posted 4 months ago

Question

\begin{array}{l} 3 x+y=3 \\ 7 x-y=2 \end{array}

\newline

The given system of equations has solution

(x, y)

. What is the value of

x

Posted 1 month ago

Question

12

-17

. What adjectives used to describe Chicago revea he poet's attitude toward the residents of the city? Describe his attitude

Posted 7 hours ago