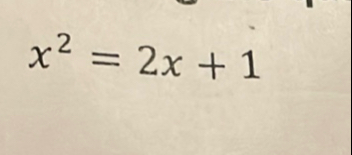Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve.
x^(2)=2x+1

Solve. $\newline$ $x^{2}=2 x+1$

View step-by-step help

View step-by-step help

Find derivatives using the chain rule I

Full solution

Q. Solve.

\newline

x^{2}=2 x+1

Identify Equation Type: Identify the type of equation. The equation $x^{2}=2x+1$ is a quadratic equation in the form of $ax^2 + bx + c = 0$ .
Rewrite in Standard Form: Rewrite the equation in standard form by subtracting $2x$ and $1$ from both sides to get $x^2 - 2x - 1 = 0$ .
Factor or Use Quadratic Formula: Attempt to factor the quadratic equation, if possible. In this case, the equation $x^2 - 2x - 1$ does not factor nicely, so we will use the quadratic formula instead. The quadratic formula is $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ , where $a = 1$ , $b = -2$ , and $c = -1$ .
Calculate Discriminant: Calculate the discriminant, which is the part under the square root in the quadratic formula: $b^2 - 4ac$ . Here, it is $(-2)^2 - 4(1)(-1) = 4 + 4 = 8$ .
Insert Values into Formula: Insert the values of $a$ , $b$ , and $c$ into the quadratic formula to find the solutions for $x$ . $x = \frac{-(-2) \pm \sqrt{(8)}}{2 \cdot 1} = \frac{2 \pm \sqrt{(8)}}{2}$ .
Simplify Solutions: Simplify the solutions. Since $\sqrt{8} = \sqrt{4\cdot2} = 2\sqrt{2}$ , the solutions are $x = \frac{2 \pm 2\sqrt{2}}{2}$ .
Final Simplification: Further simplify the solutions by dividing each term by $2$ . The final solutions are $x = 1 \pm \sqrt{2}$ .

More problems from Find derivatives using the chain rule I

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago