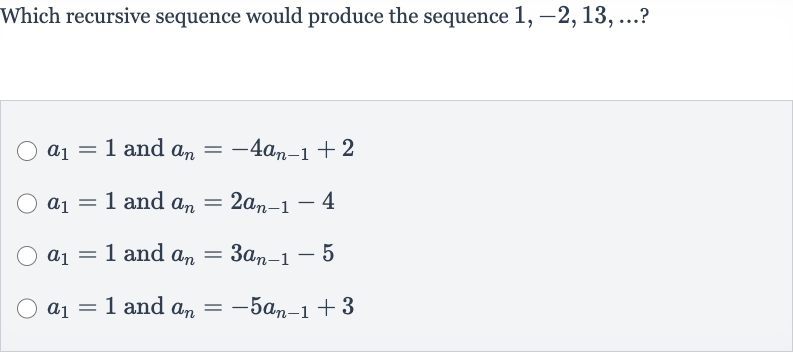Which recursive sequence would produce the sequence 1,-2,13,dots ? a_(1)=1 and a_(n)=-4a_(n-1)+2 a_(1)=1 and a_(n)=2a_(n-1)-4 a_(1)=1 and a_(n)=3a_(n-1)-5 a_(1)=1 and a_(n)=-5a_(n-1)+3

Question

Which recursive sequence would produce the sequence  1,-2,13,dots ?  a_(1)=1 and  a_(n)=-4a_(n-1)+2  a_(1)=1 and  a_(n)=2a_(n-1)-4  a_(1)=1 and  a_(n)=3a_(n-1)-5  a_(1)=1 and  a_(n)=-5a_(n-1)+3

Bytelearn · Accepted Answer

Calculate Second Term: To determine which recursive sequence produces the given sequence, we will calculate the second term using each of the provided recursive formulas and compare it to the second term in the sequence, which is -2.First Recursive Formula: Using the first recursive formula: a_(1)=1 and a_(n)=-4a_(n-1)+2. We calculate the second term: a_(2)=-4a_(1)+2 = -4*1+2 = -4+2 = -2. This matches the second term of the given sequence.Calculate Third Term: We will now calculate the third term using the same formula to see if it matches the third term of the sequence, which is 13. a_(3)=-4a_(2)+2 = -4*(-2)+2 = 8+2 = 10. This does not match the third term of the given sequence, so this recursive formula is incorrect.Second Recursive Formula: Using the second recursive formula: a_(1)=1 and a_(n)=2a_(n-1)-4. We calculate the second term: a_(2)=2a_(1)-4 = 2*1-4 = 2-4 = -2. This matches the second term of the given sequence.Calculate Third Term: We will now calculate the third term using the same formula to see if it matches the third term of the sequence, which is 13. a_(3)=2a_(2)-4 = 2*(-2)-4 = -4-4 = -8. This does not match the third term of the given sequence, so this recursive formula is also incorrect.Third Recursive Formula: Using the third recursive formula: a_(1)=1 and a_(n)=3a_(n-1)-5. We calculate the second term: a_(2)=3a_(1)-5 = 3*1-5 = 3-5 = -2. This matches the second term of the given sequence.Calculate Second Term: We will now calculate the third term using the same formula to see if it matches the third term of the sequence, which is 13. a_(3)=3a_(2)-5 = 3*(-2)-5 = -6-5 = -11. This does not match the third term of the given sequence, so this recursive formula is also incorrect.Fourth Recursive Formula: Using the fourth recursive formula: a_(1)=1 and a_(n)=-5a_(n-1)+3. We calculate the second term: a_(2)=-5a_(1)+3 = -5*1+3 = -5+3 = -2. This matches the second term of the given sequence.Calculate Third Term: We will now calculate the third term using the same formula to see if it matches the third term of the sequence, which is 13. a_(3)=-5a_(2)+3 = -5*(-2)+3 = 10+3 = 13. This matches the third term of the given sequence, so this recursive formula is correct.

Which recursive sequence would produce the sequence $1,-2,13, \ldots$ ? $\newline$ $a_{1}=1$ and $a_{n}=-4 a_{n-1}+2$ $\newline$ $a_{1}=1$ and $a_{n}=2 a_{n-1}-4$ $\newline$ $a_{1}=1$ and $a_{n}=3 a_{n-1}-5$ $\newline$ $a_{1}=1$ and $a_{n}=-5 a_{n-1}+3$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics