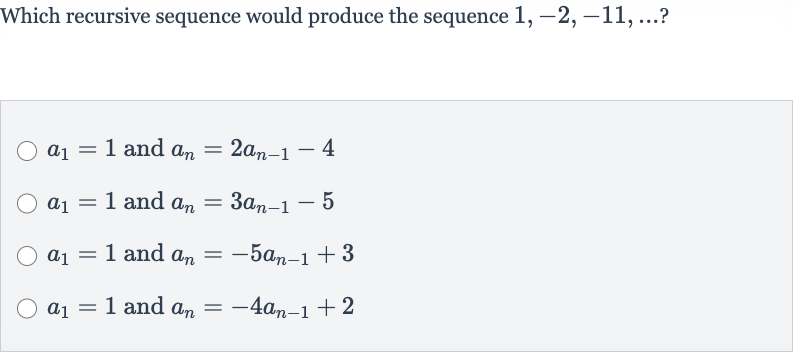Full solution
Q. Which recursive sequence would produce the sequence ? and and and and
- Test Recursive Formula: Let's start by testing each given recursive formula with the initial value to see which one produces the sequence .We will begin with the first option: and We need to calculate using the initial value .So far, the sequence matches: . Now let's calculate .The third term we calculated is , but the third term in the given sequence is . Therefore, this recursive formula does not produce the given sequence.