Full solution
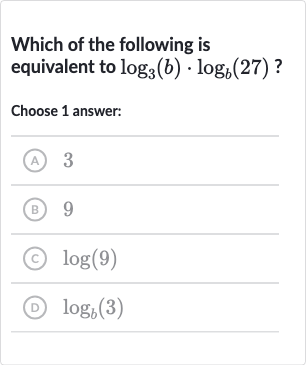
Q. Which of the following is equivalent to ?Choose answer:(A) (B) (C) (D)
- Recognize Change of Base: Recognize the use of the change of base formula. The expression involves two logarithms with different bases. We can use the change of base formula to rewrite in terms of a common base, such as base . Change of Base Formula:
- Apply Formula to log: Apply the change of base formula to . Using the change of base formula, we can write as .
- Simplify : Simplify .Since is , simplifies to .
- Substitute Simplified Value: Substitute the simplified value into the expression.Now we substitute into the expression from Step .
- Simplify the Expression: Simplify the expression.We notice that in the numerator and denominator will cancel out, leaving us with just .
More problems from Product property of logarithms
QuestionGet tutor help
QuestionGet tutor help