Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate.

(8)/(3)÷(5)/(3)=

Evaluate. $\newline$ $\frac{8}{3} \div \frac{5}{3}=$

View step-by-step help

View step-by-step help

Evaluate logarithms using a calculator

Full solution

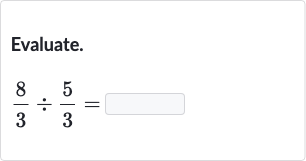
Q. Evaluate.

\newline

\frac{8}{3} \div \frac{5}{3}=

Step $1$ : Multiply by reciprocal: To divide two fractions, we multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by swapping its numerator and denominator.
Step $2$ : Perform the multiplication: The reciprocal of $(\frac{5}{3})$ is $(\frac{3}{5})$ . Now we multiply $(\frac{8}{3})$ by $(\frac{3}{5})$ .
Step $3$ : Simplify the multiplication: Perform the multiplication: $(\frac{8}{3}) \times (\frac{3}{5}) = (\frac{8 \times 3}{3 \times 5})$ .
Step $4$ : Simplify the fraction: Simplify the multiplication: $(8 \times 3) / (3 \times 5) = 24 / 15$ .
Step $5$ : Final result: Now, simplify the fraction $\frac{24}{15}$ by dividing both the numerator and the denominator by their greatest common divisor, which is $3$ .
Step $5$ : Final result: Now, simplify the fraction $\frac{24}{15}$ by dividing both the numerator and the denominator by their greatest common divisor, which is $3$ . After simplification: $(\frac{24}{3}) / (\frac{15}{3}) = \frac{8}{5}$ .
Step $5$ : Final result: Now, simplify the fraction $\frac{24}{15}$ by dividing both the numerator and the denominator by their greatest common divisor, which is $3$ . After simplification: $(\frac{24}{3}) / (\frac{15}{3}) = \frac{8}{5}$ . The fraction $\frac{8}{5}$ is the final result, and it cannot be simplified further. This is the answer to the division problem.

More problems from Evaluate logarithms using a calculator

Question

\newline

\frac{5}{6} \div \frac{9}{4}=

Posted 3 months ago

Question

\newline

\frac{5}{4} \div \frac{3}{5}=

Posted 3 months ago

Question

\newline

\frac{3}{4} \div \frac{3}{4}=

Posted 3 months ago

Question

Write the expression in exponential form.

\newline

6 \times 6 \times 6 \times 6 \times 6=

Posted 3 months ago

Question

Write the expression in exponential form.

\newline

9 \times 9 \times 9 \times 9 \times 9 \times 9 \times 9=

Posted 3 months ago

Question

The value of Vishal's car is depreciating exponentially.

\newline

The relationship between

V

, the value of his car, in dollars, and

t

, the elapsed time, in years, since he purchased the car is modeled by the following equation.

\newline

V=22,500 \cdot 10^{-\frac{t}{12}}

\newline

How many years after purchase will Vishal's car be worth

\$ 10,000

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 3 months ago

Question

A scientist measures the initial amount of Carbon

-14

in a substance to be

25

\newline

The relationship between

A

, the amount of Carbon

-14

remaining in that substance, in grams, and

t

, the elapsed time, in years, since the initial measurement is modeled by the following equation.

\newline

A=25 e^{-0.00012 t}

\newline

In how many years will the substance contain exactly

20

(\mathrm{g})

-14

\newline

Give an exact answer expressed as a natural logarithm.

\newline

Posted 3 months ago

Question

Which of the following is equivalent to

\log _{7}(a) \cdot \log _{b}(7)

\newline

1

\newline

\log (7)

\newline

\log (7 a)

\newline

\log _{a}(b)

\newline

\log _{b}(a)

Posted 3 months ago

Question

Which of the following is equivalent to

\log (a) \cdot \log _{a}(5)

\newline

1

\newline

\log (a)

\newline

\log (5)

\newline

\log (5 a)

\newline

\log _{a}(5 a)

Posted 3 months ago

Question

8

) How many liters of pure water should be added to

150

35\%

salt water saline solution to make it a

25\%

salt water saline solution? Let

\quad = \quad

\quad 11 =\quad

Posted 4 hours ago