Full solution

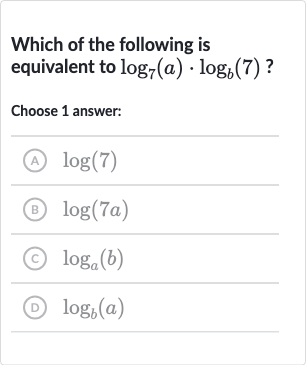
Q. Which of the following is equivalent to

\log _{7}(a) \cdot \log _{b}(7)

\newline

Choose

1

answer:

\newline

(A)

\log (7)

\newline

(B)

\log (7 a)

\newline

(C)

\log _{a}(b)

\newline

(D)

\log _{b}(a)

Recognize change of base formula: Recognize the use of the change of base formula. $\newline$ The expression $\log_{7}(a)\cdot\log_{b}(7)$ suggests the use of the change of base formula, which is $\log_{c}(a) = \frac{\log_d(a)}{\log_d(c)}$ for any positive numbers $a$ , $c$ , and $d$ (where $a, c \neq 1$ ).
Apply change of base formula to log: Apply the change of base formula to $\log_{b}(7)$ . $\newline$ We can rewrite $\log_{b}(7)$ using the change of base formula with a new base, which we'll choose as 'a'. This gives us $\log_{b}(7) = \frac{\log_{a}(7)}{\log_{a}(b)}$ .
Substitute expression from Step $2$ : Substitute the expression from Step $2$ into the original expression. $\newline$ Now we replace $\log_{b}(7)$ in the original expression with the result from Step $2$ , which gives us $\log_{7}(a) \cdot \left(\frac{\log_{a}(7)}{\log_{a}(b)}\right)$ .
Simplify the expression: Simplify the expression. $\newline$ We notice that $\log_{7}(a)$ and $\log_{a}(7)$ are inverses of each other, meaning their product is $1$ . So, the expression simplifies to $\frac{1}{\log_{a}(b)}$ .
Recognize simplified expression as a logarithm: Recognize the simplified expression as a logarithm. $\newline$ The expression $\frac{1}{\log_a(b)}$ is the same as $\log_{b}(a)$ by the definition of the reciprocal of a logarithm.
Match simplified expression to answer choices: Match the simplified expression to the answer choices. $\newline$ The expression $\log_{b}(a)$ corresponds to answer choice (D).