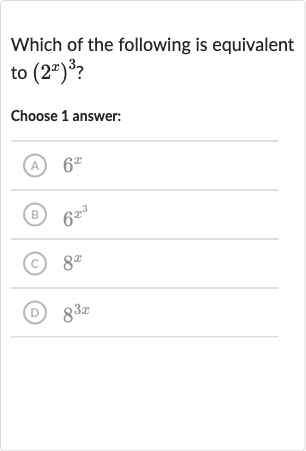
Which of the following is equivalent to (2^(x))^(3) ? Choose 1 answer: (A) 6^(x) (B) 6x^(x^(3)) (C) 8^(x) (D) 8^(3x)

Question

Which of the following is equivalent to  (2^(x))^(3) ? Choose 1 answer: (A)  6^(x) (B)  6x^(x^(3)) (C)  8^(x) (D)  8^(3x)

Bytelearn · Accepted Answer

Apply Exponentiation Rule: To solve this problem, we need to apply the exponentiation rule which states that (a^(b))^c = a^(b*c). In this case, a = 2, b = x, and c = 3.Calculate Simplified Expression: Using the exponentiation rule, we calculate (2^(x))^(3) = 2^(x*3).Compare with Given Options: Simplify the expression 2^(x*3) to get 2^(3x).Option (A): Now we compare the simplified expression 2^(3x) with the given options to find the equivalent one.Option (B): Option (A) is 6^(x), which is not equivalent to 2^(3x) because 6 is not a power of 2.Option (C): Option (B) is 6x^(x^(3)), which is not equivalent to 2^(3x) because it involves multiplication and a different base.Option (D): Option (C) is 8^(x), which is not equivalent to 2^(3x) because 8^(x) is the same as (2^3)^(x) = 2^(3x), but we need the exponent to be 3x, not x.Option (D) is 8^(3x), which is equivalent to 2^(3x) because 8 is 2^3, so 8^(3x) is the same as (2^3)^(3x) = 2^(3*3x) = 2^(9x), which is not the same as 2^(3x).

Which of the following is equivalent to $\newline$ $(2^{x})^{3}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $6^{x}$ $\newline$ (B) $6x^{x^{3}}$ $\newline$ (C) $8^{x}$ $\newline$ (D) $8^{3x}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Which of the following is equivalent to \newline(2x)3(2^{x})^{3}(2x)3 ?\newlineChoose 111 answer:\newline(A) 6x6^{x}6x\newline(B) 6xx36x^{x^{3}}6xx3\newline(C) 8x8^{x}8x\newline(D) 83x8^{3x}83x

Which of the following is equivalent to $\newline$ $(2^{x})^{3}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $6^{x}$ $\newline$ (B) $6x^{x^{3}}$ $\newline$ (C) $8^{x}$ $\newline$ (D) $8^{3x}$