Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which of the following is equivalent to (1)/(log_(3)(m)) ? Choose 1 answer: (A) log_(m)(3) (B) log_(3)(m) (C) -log_(m)(3) (D) -log_(3)(m)

Which of the following is equivalent to 1log⁡3(m) \frac{1}{\log _{3}(m)} ?\newlineChoose 11 answer:\newline(A) log⁡m(3) \log _{m}(3) \newline(B) log⁡3(m) \log _{3}(m) \newline(C) −log⁡m(3) -\log _{m}(3) \newline(D) −log⁡3(m) -\log _{3}(m)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Product property of logarithmsright chevron icon

Full solution

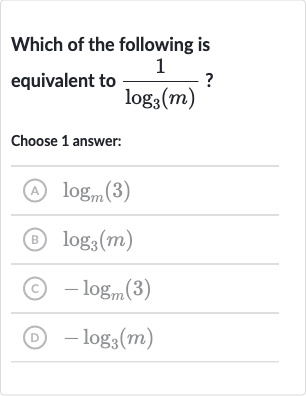
Q. Which of the following is equivalent to 1log⁡3(m) \frac{1}{\log _{3}(m)} ?\newlineChoose 11 answer:\newline(A) log⁡m(3) \log _{m}(3) \newline(B) log⁡3(m) \log _{3}(m) \newline(C) −log⁡m(3) -\log _{m}(3) \newline(D) −log⁡3(m) -\log _{3}(m)
  1. Recognize relationship between reciprocal and change of base: Recognize the relationship between the reciprocal of a logarithm and the change of base formula.\newlineThe reciprocal of a logarithm can be expressed using the change of base formula. The change of base formula states that log⁡b(a)=log⁡c(a)log⁡c(b)\log_b(a) = \frac{\log_c(a)}{\log_c(b)}, where bb and cc are bases and aa is the argument of the logarithm.
  2. Apply change of base formula: Apply the change of base formula to the given expression.\newlineWe have (1)/(log⁡3(m))(1)/(\log_{3}(m)). According to the change of base formula, this can be rewritten as log⁡m(3)\log_m(3) because log⁡m(3)=log⁡3(3)log⁡3(m)=1log⁡3(m)\log_m(3) = \frac{\log_3(3)}{\log_3(m)} = \frac{1}{\log_3(m)}.
  3. Match result with given options: Match the result with the given options.\newlineThe expression log⁡m(3)\log_m(3) matches with option (A) log⁡m(3)\log_{m}(3).

More problems from Product property of logarithms

Question
Evaluate.\newline56÷94= \frac{5}{6} \div \frac{9}{4}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate.\newline83÷53= \frac{8}{3} \div \frac{5}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate.\newline54÷35= \frac{5}{4} \div \frac{3}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate.\newline34÷34= \frac{3}{4} \div \frac{3}{4}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the expression in exponential form.\newline6×6×6×6×6= 6 \times 6 \times 6 \times 6 \times 6=
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the expression in exponential form.\newline9×9×9×9×9×9×9= 9 \times 9 \times 9 \times 9 \times 9 \times 9 \times 9=
Get tutor helpright-arrow

Posted 3 months ago

Question
The value of Vishal's car is depreciating exponentially.\newlineThe relationship between V V , the value of his car, in dollars, and t t , the elapsed time, in years, since he purchased the car is modeled by the following equation.\newlineV=22,500⋅10−t12 V=22,500 \cdot 10^{-\frac{t}{12}} \newlineHow many years after purchase will Vishal's car be worth $10,000 \$ 10,000 ?\newlineGive an exact answer expressed as a base−10-10 logarithm.\newlineyears
Get tutor helpright-arrow

Posted 3 months ago

Question
A scientist measures the initial amount of Carbon−14-14 in a substance to be 2525 grams.\newlineThe relationship between A A , the amount of Carbon−14-14 remaining in that substance, in grams, and t t , the elapsed time, in years, since the initial measurement is modeled by the following equation.\newlineA=25e−0.00012t A=25 e^{-0.00012 t} \newlineIn how many years will the substance contain exactly 2020 grams (g) (\mathrm{g}) of Carbon−14-14?\newlineGive an exact answer expressed as a natural logarithm.\newlineyears
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following is equivalent to log⁡7(a)⋅log⁡b(7) \log _{7}(a) \cdot \log _{b}(7) ?\newlineChoose 11 answer:\newline(A) log⁡(7) \log (7) \newline(B) log⁡(7a) \log (7 a) \newline(C) log⁡a(b) \log _{a}(b) \newline(D) log⁡b(a) \log _{b}(a)
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following is equivalent to log⁡(a)⋅log⁡a(5) \log (a) \cdot \log _{a}(5) ?\newlineChoose 11 answer:\newline(A) log⁡(a) \log (a) \newline(B) log⁡(5) \log (5) \newline(C) log⁡(5a) \log (5 a) \newline(D) log⁡a(5a) \log _{a}(5 a)
Get tutor helpright-arrow

Posted 3 months ago

View all (17)