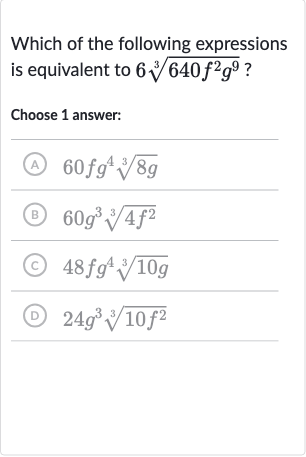
Which of the following expressions is equivalent to 6root(3)(640f^(2)g^(9)) ? Choose 1 answer: (A) 60 fg^(4)root(3)(8g) (B) 60g^(3)root(3)(4f^(2)) (C) 48 fg^(4)root(3)(10 g) (D) 24g^(3)root(3)(10f^(2))

Question

Which of the following expressions is equivalent to  6root(3)(640f^(2)g^(9)) ? Choose 1 answer: (A)  60 fg^(4)root(3)(8g) (B)  60g^(3)root(3)(4f^(2)) (C)  48 fg^(4)root(3)(10 g) (D)  24g^(3)root(3)(10f^(2))

Bytelearn · Accepted Answer

Simplify Inside Cube Root: First, let's simplify the inside of the cube root. 640 can be broken down into prime factors: 640 = 2^7 * 5.Take Out Perfect Cubes: Now, let's take out everything that's a perfect cube. 2^7 can be broken down into 2^6 * 2, where 2^6 is a perfect cube (2^2)^3. So we can take 2^2 out of the cube root.Factor Out g^9: For g^9, since 9 is a multiple of 3, we can take g^3 out of the cube root.Final Simplification: Now we have 6 * 2^2 * g^3 * cube root of (2 * 5 * f^2). This simplifies to 6 * 4 * g^3 * cube root of (10f^2).Multiply and Simplify: Multiplying 6 by 4 gives us 24. So we have 24g^3 * cube root of (10f^2).Match with Answer Choices: Looking at the answer choices, the expression that matches our result is (D) 24g^(3)root(3)(10f^(2)).

Which of the following expressions is equivalent to $\newline$ $6\sqrt[3]{640f^{2}g^{9}}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $60 fg^{4}\sqrt[3]{8g}$ $\newline$ (B) $60g^{3}\sqrt[3]{4f^{2}}$ $\newline$ (C) $48 fg^{4}\sqrt[3]{10 g}$ $\newline$ (D) $24g^{3}\sqrt[3]{10f^{2}}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics