Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

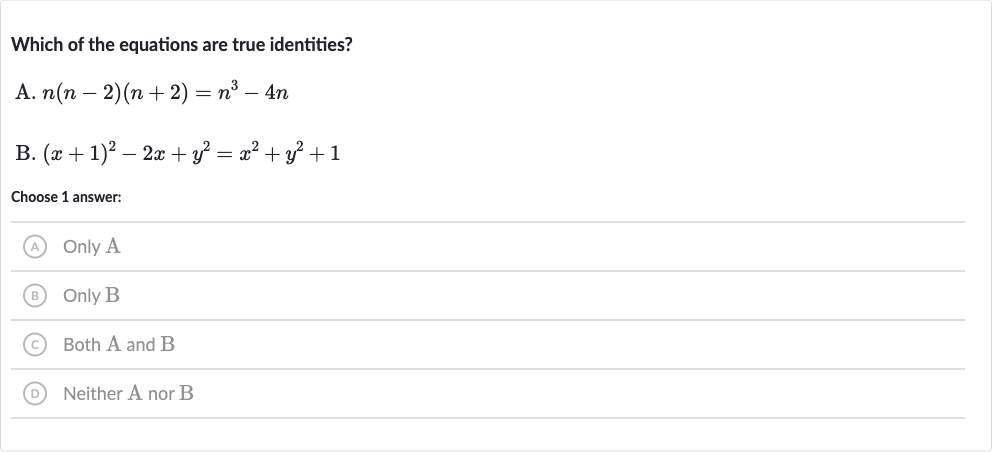
Which of the equations are true identities?
A.
n(n-2)(n+2)=n^(3)-4n
B.
(x+1)^(2)-2x+y^(2)=x^(2)+y^(2)+1
Choose 1 answer:
(A) Only A
(B) Only B
(C) Both A and B
(D) Neither A nor B

Which of the equations are true identities? $\newline$ A. $n(n-2)(n+2)=n^{3}-4 n$ $\newline$ B. $(x+1)^{2}-2 x+y^{2}=x^{2}+y^{2}+1$ $\newline$ Choose $1$ answer: $\newline$ (A) Only A $\newline$ (B) Only B $\newline$ (C) Both A and B $\newline$ (D) Neither A nor B

View step-by-step help

View step-by-step help

Full solution

Q. Which of the equations are true identities?

\newline

A.

n(n-2)(n+2)=n^{3}-4 n

\newline

B.

(x+1)^{2}-2 x+y^{2}=x^{2}+y^{2}+1

\newline

Choose

1

answer:

\newline

(A) Only A

\newline

(B) Only B

\newline

(C) Both A and B

\newline

(D) Neither A nor B

Expand A: Expand $A: n(n-2)(n+2)$ . $n(n^2 - 2n + 2n - 4) = n(n^2 - 4)$ .
Simplify expression: Simplify the expression. $n(n^2 - 4) = n^3 - 4n$ .
Check identity for $A$ : Check if $A$ is an identity. $n(n-2)(n+2) = n^3 - 4n$ is true.
Expand B: Expand B: $(x+1)^2 - 2x + y^2$ . $x^2 + 2x + 1 - 2x + y^2 = x^2 + y^2 + 1$ .
Check identity for B: Check if B is an identity. $\newline$ $(x+1)^2 - 2x + y^2 = x^2 + y^2 + 1$ is true.

More problems from Power rule

Question

h(x)=\log _{2}(x)

\newline

Can we use the mean value theorem to say the equation

h^{\prime}(x)=1

has a solution where

1<x<2

\newline

1

\newline

(A) No, since the function is not differentiable on that interval.

\newline

(B) No, since the average rate of change of

h

over the interval

1 \leq x \leq 2

1

\newline

(C) Yes, both conditions for using the mean value theorem have been met.

Posted 3 months ago

Question

What is the sign of

39 \frac{11}{13}+\left(-41 \frac{1}{13}\right) \text { ? }

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

What is the sign of

-1042+1042 ?

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

What is the sign of

-18 \frac{9}{17}+\left(-18 \frac{9}{17}\right)

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

What is the sign of

\frac{23}{45}+\left(-\frac{23}{45}\right) ?

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

What is the sign of

45+(-38)

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

What is the sign of

-49.8+61.2

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

What is the sign of

-1.69+(-1.69) ?

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

What is the sign of

37+(-37)

\newline

1

\newline

\newline

\newline

(C) Neither positive nor negative-the sum is zero.

Posted 3 months ago

Question

\begin{array}{l} g(x)=\sqrt{2 x-9} \\ g^{\prime}(x)=? \end{array}

\newline

1

\newline

\frac{\sqrt{2 x-9}}{2}

\newline

\frac{1}{\sqrt{2 x-9}}

\newline

\frac{1}{2 \sqrt{2 x-9}}

\newline

\frac{1}{\sqrt{x}}

Posted 3 months ago