AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
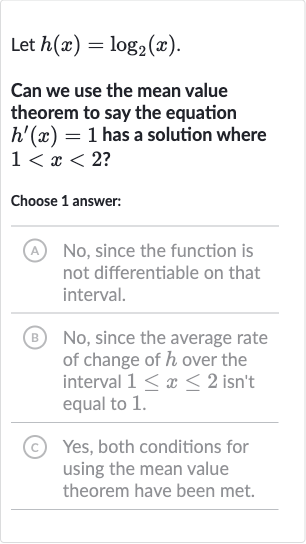
Let .Can we use the mean value theorem to say the equation has a solution where \( 1
Full solution
Q. Let .Can we use the mean value theorem to say the equation has a solution where ?Choose answer:(A) No, since the function is not differentiable on that interval.(B) No, since the average rate of change of over the interval isn't equal to .(C) Yes, both conditions for using the mean value theorem have been met.
- Recall Mean Value Theorem: First, let's recall the mean value theorem (MVT). The MVT states that if a function is continuous on a closed interval and differentiable on the open interval , then there exists at least one in such that .
- Check Function Conditions: Now, let's check if the function meets the conditions of the MVT on the interval . The function is continuous and differentiable on the interval because the logarithmic function is continuous and differentiable for all positive values.
- Calculate Average Rate of Change: Next, we calculate the average rate of change of over the interval . This is given by .
- Find and : We calculate and . Since , we have and .
- Calculate Average Rate of Change: Now, we find the average rate of change: .
- Apply Mean Value Theorem: Since the average rate of change of over the interval is equal to , and the function is continuous and differentiable on that interval, both conditions for using the mean value theorem have been met.
- Apply Mean Value Theorem: Since the average rate of change of over the interval is equal to , and the function is continuous and differentiable on that interval, both conditions for using the mean value theorem have been met.Therefore, by the mean value theorem, there exists at least one in the interval such that .
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
