Full solution
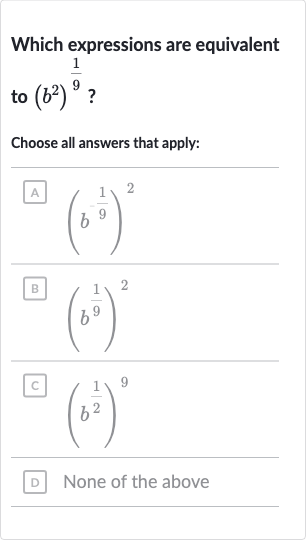
Q. Which expressions are equivalent to ?Choose all answers that apply: None of the above
- Understand Exponent Properties: Understand the properties of exponents.When an exponent is raised to another exponent, you multiply the exponents.
- Compare with Simplified Expression: Compare the given options with the simplified expression . Option A: , which is not equal to .
- Check Option A: Check option B.Option B: , which is equal to .
- Check Option B: Check option C.Option C: , which is not equal to .
- Check Option C: Determine the correct answers based on the calculations.Only option B is equivalent to .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help