Full solution
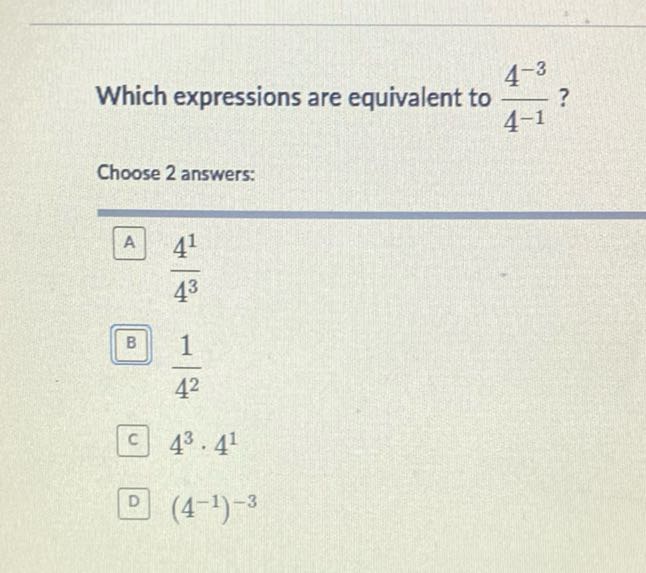
Q. Which expressions are equivalent to ?Choose answers:(A) (B) c. D
- Simplify Exponential Expression: Simplify the given expression using the properties of exponents.When dividing exponential expressions with the same base, subtract the exponents.
- Compare with Options: Compare the simplified expression with the given options.We have simplified the expression to . Now we need to see which options are equivalent to this expression.Option (A) simplifies to .Option (B) is already in the form .Option (C) simplifies to , which is not equivalent.Option (D) simplifies to , which is not equivalent.
- Identify Correct Options: Identify the correct options.From Step , we can see that Option (A) and Option (B) are equivalent to the simplified expression .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help