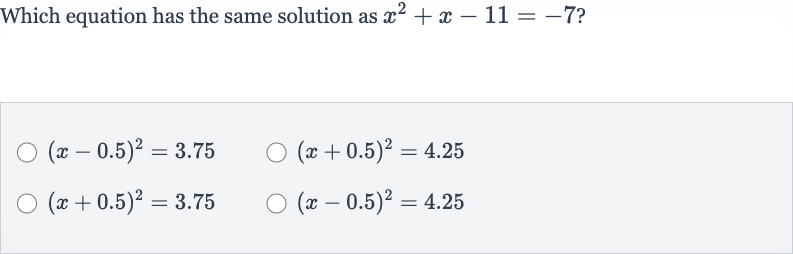Which equation has the same solution as x^(2)+x-11=-7 ? (x-0.5)^(2)=3.75 (x+0.5)^(2)=4.25 (x+0.5)^(2)=3.75 (x-0.5)^(2)=4.25

Question

Which equation has the same solution as  x^(2)+x-11=-7 ?  (x-0.5)^(2)=3.75  (x+0.5)^(2)=4.25  (x+0.5)^(2)=3.75  (x-0.5)^(2)=4.25

Bytelearn · Accepted Answer

Simplify the Equation: First, we need to simplify the given equation x^2 + x - 11 = -7 by adding 7 to both sides to isolate the x terms on one side. x^2 + x - 11 + 7 = -7 + 7 x^2 + x - 4 = 0Check First Option: Now, we need to determine which of the provided equations, when simplified or expanded, will result in the same quadratic equation as x^2 + x - 4 = 0. Let's start with the first option: (x - 0.5)^2 = 3.75. Expanding (x - 0.5)^2 gives us: (x - 0.5)(x - 0.5) = x^2 - x + 0.25 This does not match our simplified equation x^2 + x - 4.Check Second Option: Next, let's consider the second option: (x + 0.5)^2 = 4.25. Expanding (x + 0.5)^2 gives us: (x + 0.5)(x + 0.5) = x^2 + x + 0.25 This also does not match our simplified equation x^2 + x - 4.Check Third Option: Now, let's look at the third option: (x + 0.5)^2 = 3.75. Expanding (x + 0.5)^2 gives us: (x + 0.5)(x + 0.5) = x^2 + x + 0.25 To match our simplified equation x^2 + x - 4, we need to see if 0.25 is equal to 3.75 when we move it to the other side of the equation. x^2 + x + 0.25 - 0.25 = 3.75 - 0.25 x^2 + x = 3.5 This does not match our simplified equation x^2 + x - 4.Check Fourth Option: Finally, let's examine the fourth option: (x - 0.5)^2 = 4.25. Expanding (x - 0.5)^2 gives us: (x - 0.5)(x - 0.5) = x^2 - x + 0.25 To match our simplified equation x^2 + x - 4, we need to see if 0.25 is equal to 4.25 when we move it to the other side of the equation. x^2 - x + 0.25 - 0.25 = 4.25 - 0.25 x^2 - x = 4 This does not match our simplified equation x^2 + x - 4 either.Reevaluate Third Option: It seems that none of the provided options exactly match the simplified equation x^2 + x - 4 = 0. However, we may have made a mistake in our calculations. Let's recheck the third option: (x + 0.5)^2 = 3.75. Expanding (x + 0.5)^2 gives us: (x + 0.5)(x + 0.5) = x^2 + x + 0.25 Now, subtracting 0.25 from both sides to match our simplified equation: x^2 + x + 0.25 - 0.25 = 3.75 - 0.25 x^2 + x = 3.5 This is incorrect, as we need the constant term to be -4, not 3.5. Therefore, there is a math error in our previous step.

Which equation has the same solution as $x^{2}+x-11=-7$ ? $\newline$ $(x-0.5)^{2}=3.75$ $\newline$ $(x+0.5)^{2}=4.25$ $\newline$ $(x+0.5)^{2}=3.75$ $\newline$ $(x-0.5)^{2}=4.25$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics