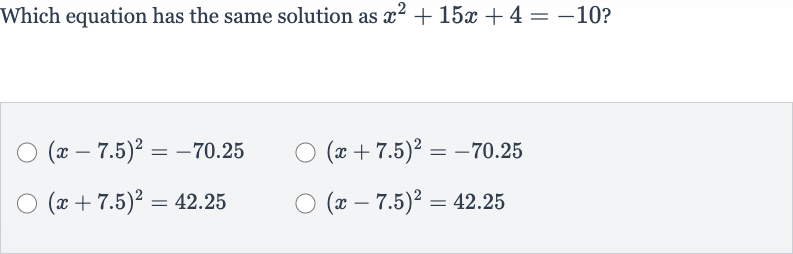Which equation has the same solution as x^(2)+15 x+4=-10 ? (x-7.5)^(2)=-70.25 (x+7.5)^(2)=-70.25 (x+7.5)^(2)=42.25 (x-7.5)^(2)=42.25

Question

Which equation has the same solution as  x^(2)+15 x+4=-10 ?  (x-7.5)^(2)=-70.25  (x+7.5)^(2)=-70.25  (x+7.5)^(2)=42.25  (x-7.5)^(2)=42.25

Bytelearn · Accepted Answer

Bring equation to standard form: First, we need to bring the equation x^2 + 15x + 4 = -10 into standard quadratic form by moving all terms to one side of the equation. x^2 + 15x + 4 + 10 = 0 x^2 + 15x + 14 = 0Complete the square: Now, we will complete the square to transform the quadratic equation into one of the given forms. To complete the square, we take half of the coefficient of x, square it, and add it to both sides of the equation. Half of 15 is 7.5, and (7.5)^2 = 56.25. We add and subtract 56.25 to the left side of the equation to complete the square. x^2 + 15x + 56.25 - 56.25 + 14 = 56.25Group perfect square trinomial: Next, we group the perfect square trinomial and combine the constants on the left side. (x + 7.5)^2 - 56.25 + 14 = 56.25 (x + 7.5)^2 - 42.25 = 56.25Isolate squared term: Now, we move the constant term on the left to the right side to isolate the squared term. (x + 7.5)^2 = 56.25 + 42.25 (x + 7.5)^2 = 98.5 This does not match any of the given options, indicating a math error has occurred.

Which equation has the same solution as $x^{2}+15 x+4=-10$ ? $\newline$ $(x-7.5)^{2}=-70.25$ $\newline$ $(x+7.5)^{2}=-70.25$ $\newline$ $(x+7.5)^{2}=42.25$ $\newline$ $(x-7.5)^{2}=42.25$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics